Next: Brianchon's Theorem
Up: Projective Conics

Pascal's Theorem

We use this diagram to construct the points on a point conic:

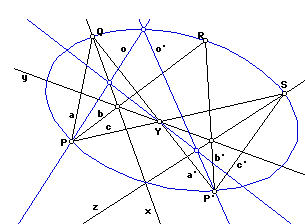
We are given five points P, P', Q, R, and S, and can show that the conic lying on these five points was given by the locus of blue points.

Now let us define N as the intersection of x and z. We see in the diagram that N is on the conic, and can verify that our construction would send PN to P'N. We can state this as a theorem:

If PR.QN, RP'.NS, and P'Q.SP are collinear, then N lies on the conic determined by PP'QRS.

Rather than saying that N lies on the conic determined by PP'QRS, we could simply say that NPP'QRS lie on a conic. It will also simplify things to speak about the hexagon PRP'QNS; then the points lie on a conic if and only if the hexagon is inscribed in that conic. Making these modifications and some changes of labelling, we have the theorem:

If opposite sides of a hexagon (ABCDEF) intersect in three points (AB.DE, BC.EF, CD.FA) which are collinear, then the hexagon may be inscribed in a conic.

This is known as the converse of Pascal's theorem.

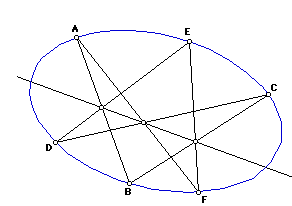
So Pascal's theorem says:

If a hexagon (ABCDEF) is inscribed in a conic, then opposite sides intersect in three points (AB.DE, BC.EF, CD.FA) which are collinear.

Proof: Define L=BC.EF, M=CD.FA, N=AB.DE; we want to show L, M, N collinear. To do this, we also define J=AB.CD, K=FA.BC. Then 

( A, N; J, B) =
(DA,DE;DC,DB) =
(FA,FE;FC,FB) =
( K, L; C, B).
Thus the projectivity sending A to K, J to C, and B to B must also send N to L. Since that projectivity is the perspectivity defined by M, M sends N to L; in other words, L, M, and N are collinear as desired. We may say that they lie on the Pascal line of the hexagon.

Note that Pascal's theorem is true regardless of where the points lie on the conic. The diagram above shows a very non-convex hexagon, but since projective geometry does not deal with convexity, a convex hexagon would do just as well. However, a convex hexagon might have a Pascal line too far off the diagram to be seen.

Next: Brianchon's Theorem
Up: Projective Conics
[HOME] The Geometry Center Home Page

Comments to: webmaster@geom.umn.edu
Created: Nov 30 1995 --- Last modified: Thu Nov 30 15:31:14 1995