The celestial image of a polyhedron
Next: Clocks and curvature
Up: Geometry and the Imagination
Previous: Gaussian curvature
We want now to discuss the celestial image of a polyhedron,
and use it to get yet another proof of Descartes's angle-defect formula.
-
What pattern is traced out on the celestial sphere when you move a
flashlight around on the surface of a cube, keeping its tail as flat
as possible on the surface? What is the celestial pattern for a dodecahedron?
-
On a convex polyhedron,
the celestial image of a region containing a solitary vertex
 where three faces
meet is a triangle.
Show that the three angles of this celestial triangle
are the supplements of the angles of the three faces
that meet at
where three faces
meet is a triangle.
Show that the three angles of this celestial triangle
are the supplements of the angles of the three faces
that meet at  .
.
-
Show that the area of this celestial triangle is the angle defect at
 .
.
-
Show that the total angle defect of a convex polyhedron is
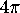 .
.
Next: Clocks and curvature
Up: Geometry and the Imagination
Previous: Gaussian curvature
Peter Doyle
 where three faces
meet is a triangle.
Show that the three angles of this celestial triangle
are the supplements of the angles of the three faces
that meet at
where three faces
meet is a triangle.
Show that the three angles of this celestial triangle
are the supplements of the angles of the three faces
that meet at  .
.
 .
.
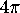 .
.
 where three faces
meet is a triangle.
Show that the three angles of this celestial triangle
are the supplements of the angles of the three faces
that meet at
where three faces
meet is a triangle.
Show that the three angles of this celestial triangle
are the supplements of the angles of the three faces
that meet at  .
.
 .
.
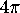 .
.