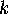 , then the Euler characteristic of the quotient orbifold is
, then the Euler characteristic of the quotient orbifold is 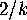 ,
since the Euler characteristic of the sphere is 2.
,
since the Euler characteristic of the sphere is 2.
A symmetry pattern on the sphere always gives rise to a quotient orbifold
with positive Euler characteristic. In fact, if the order of symmetry is
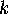 , then the Euler characteristic of the quotient orbifold is
, then the Euler characteristic of the quotient orbifold is 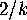 ,
since the Euler characteristic of the sphere is 2.
,
since the Euler characteristic of the sphere is 2.
However, the converse is not true. Not every collection of parts costing
less than 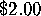 can be put together to make a viable pattern for
symmetry on the sphere. Fortunately, the experts at The Orbifold Shop
know the four bad configurations which are too skimpy to be viable:
can be put together to make a viable pattern for
symmetry on the sphere. Fortunately, the experts at The Orbifold Shop
know the four bad configurations which are too skimpy to be viable:
All other configurations are good. If they form an orbifold with positive orbifold Euler characteristic, they come from a pattern of symmetry on the sphere.
The situation for negative orbifold Euler characteristic is straightforward, but we will not prove it:
Theorem. Every orbifold with negative orbifold Euler characteristic comes from a pattern of symmetry in the hyperbolic plane with bounded fundamental domain. Every pattern of symmetry in the hyperbolic plane with compact fundamental domain gives rise to a quotient orbifold with negative orbifold Euler characteristic.
Since you can spend as much as you want, there are an infinite number of these.