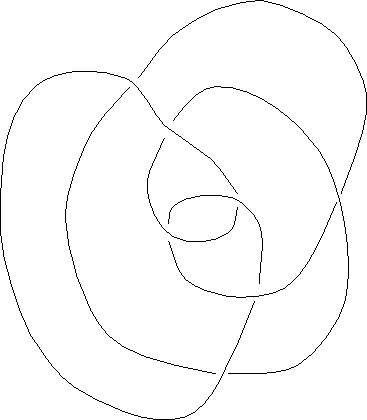
Figure 1: This is drawing of a knot has 7 crossings. Is it possible to rearrange it to have fewer crossings?
A mathematical knot is a knotted loop. For example, you might take an extension cord from a drawer and plug one end into the other: this makes a mathematical knot.
It might or might not be possible to unknot it without unplugging the cord. A knot which can be unknotted is called an unknot.
Two knots are considered equivalent if it is possible to rearrange one to the form of the other, without cutting the loop and without allowing it to pass through itself. The reason for using loops of string in the mathematical definition is that knots in a length of string can always be undone by pulling the ends through, so any two lengths of string are equivalent in this sense.
If you drop a knotted loop of string on a table, it crosses over itself in a certain number of places. Possibly, there are ways to rearrange it with fewer crossings-the minimum possible number of crossings is the crossing number of the knot.
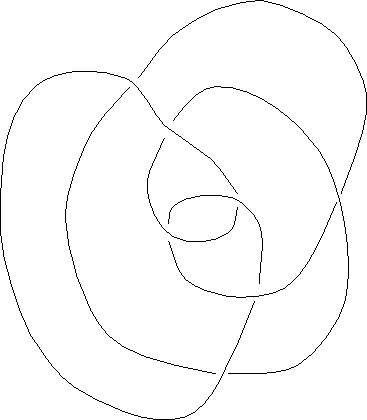
Figure 1: This is drawing of a knot has 7
crossings. Is it possible to rearrange it to have fewer crossings?
Make drawings and use short lengths of string to investigate simple knots: