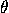 be the angle
at any vertex, r and R the radii of the inscribed and
circumscribed circles (r is called the apothem). As usual, let
s=½ka be the half-perimeter. Then:
be the angle
at any vertex, r and R the radii of the inscribed and
circumscribed circles (r is called the apothem). As usual, let
s=½ka be the half-perimeter. Then:
Next: 6 Circles
Up: 5 Polygons
Previous: 5.2 Quadrilaterals
A polygon is regular if all its sides are equal and all its angles are equal. Either condition implies the other in the case of a triangle, but not in general. (A rhombus has equal sides but not necessarily equal angles, and a rectangle has equal angles but not necessarily equal sides.)
For a k-sided regular polygon of side a, let 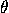 be the angle
at any vertex, r and R the radii of the inscribed and
circumscribed circles (r is called the apothem). As usual, let
s=½ka be the half-perimeter. Then:
be the angle
at any vertex, r and R the radii of the inscribed and
circumscribed circles (r is called the apothem). As usual, let
s=½ka be the half-perimeter. Then:
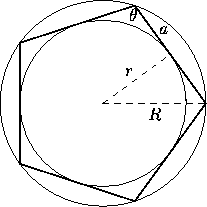

If 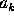 denotes the side of a k-sided regular polygon
inscribed in a circle of radius R, we have
denotes the side of a k-sided regular polygon
inscribed in a circle of radius R, we have

If 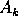 denotes the side of a k-sided regular polygon
circumscribed about the same circle, we have
denotes the side of a k-sided regular polygon
circumscribed about the same circle, we have

In particular,
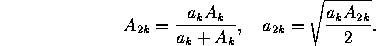
The areas 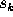 ,
,  ,
,  and
and 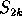 of the same polygons
satisfy
of the same polygons
satisfy
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.