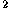Next: 8 Special Plane Curves
Up: 7 Conics
Previous: 7.4 Additional Properties of Hyperbolas

7.5 Additional Properties of Parabolas

Let C be the parabola with equation y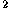=4ax, and let F=(a,0) be its focus.

• Let P=(x,y) and P'=(x',y') be points on C. The area bounded by the chord PP' and the corresponding arc of the parabola is

  

  It equals four-thirds of the area of the triangle PQP', where Q is the point on C whose tangent is parallel to the chord PP' (formula due to Archimedes).

• The length of the arc from (0,0) to the point (x,y) is

  

• The polar equation for C in the usual polar coordinate system is

  

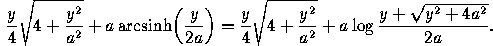
  With respect to a coordinate system with origin at F the equation is

  

  where l=2a is half the latus rectum.

• Let P be any point of C. Then the ray PF and the horizontal line through P make the same angle with the tangent to C at P. Thus light rays parallel to the axis and reflected in the parabola converge onto F (principle of the parabolic reflector).

The Geometry Center Home Page

Silvio Levy
Wed Oct 4 16:41:25 PDT 1995

This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.