Next: 11.3 Projective Transformations
Up: 11 Other Transformations of Space
Previous: 11.1 Similarities

11.2 Affine Transformations

A transformation that preserves lines and parallelism (maps parallel lines to parallel lines) is an affine transformation. There are two important particular cases of such transformations:

A nonproportional scaling transformation centered at the origin has the form

(x,y,z)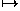(ax,by,cz),

where a,b,c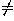0 are the scaling factors (real numbers). The corresponding matrix in homogeneous coordinates is

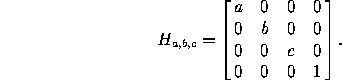
A shear in the x-direction and preserving horizontal planes has the form

(x,y,z)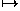(x+rz,y,z),

where r is the shearing factor. The corresponding matrix in homogeneous coordinates is

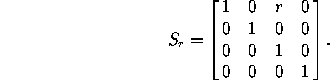
Every affine transformation is obtained by composing a scaling transformation with an isometry, or one or two shears with a homothety and an isometry.

The Geometry Center Home Page

Silvio Levy
Wed Oct 4 16:41:25 PDT 1995

This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.