Image of a Klein bottle with color coded 4D depth and ribbon slicing to reveal interior structure. (T. Banchoff and N. Thompson, Brown University.)
This semi-transparent Klein bottle displayed by Fourphront contains a Möbius band (opaque). The projection of the surface to 3D contains an intersection line, highlighted in black. (D. Banks, University of North Carolina and Langley Research Center.)
A snapshot from an interactive sequence showing the deformation of a Möbius band with 3 half-twists into Ulrich Brehm's trefoil knotbox. (G. Chappell, G. Francis and C. Hartman, University of Illinois at Urbana-Champaign.)
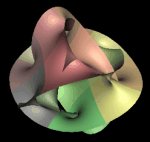
The n=4 Fermat surface projected to 3D using the MeshView interactive 4D viewer. The colors encode the relative complex phase of different patches of the surface. (H. Ma and A. Hanson, Indiana University.)
An application of slicing, projection, and color-coding to exhibit the properties of a knotted sphere in 4D space.
A cutaway view of a knotted sphere with 4D-depth-dependent texture map density.
Illustration of
cutaway and above-below
crossing markings for
the twist-spun trefoil, a surface embedded 4D that, surprisingly, is
actually not knotted. (Frames from the video animation ``knot
,''
Indiana University.)
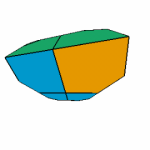
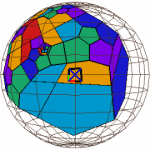
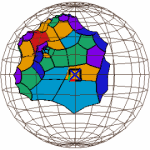
A partial tessellation of regular right-angled dodecahedra in the three built-in Geomview models (virtual, projective, and conformal, respectively) of hyperbolic 3-space. (Geometry Center.)
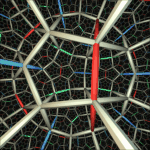
A view of the tessellation of hyperbolic space by regular right-angled dodecahedra. (Frame from the movie ``Not Knot''; C. Gunn, Geometry Center.)
Evolver/Geomview display of spacecraft fuel tank; the fuel surface tension computed with the Evolver is the only force available to guide fuel to the intake valve in low gravity. (K. Brakke, Susquehanna University.)
The minimal surfaces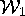 
,
periodic with quotient genus one, and
, which is
nonperiodic of genus one. These surfaces were discovered with the aid
of computer graphics techniques. (D. Hoffman, University of
Massachusetts, Amherst.)
Using Maniview, an external module of Geomview, the user can fly around in the insider's view of the 3D Klein bottle. Note that spaceships in alternating columns are mirror reversed. (C. Fowler and C. Gunn, Geometry Center.)
Images of 4D-lit knotted spheres including depiction of 4D occlusion in the 3D projection; this is similar to the self-occlusions of a knotted rope in 3D projected to a 2D image. The first image is a time-consuming volume rendering, while its equivalent below can be manipulated using real-time methods. (R. Cross, A. Hanson, and P. Heng, Indiana University.)
A frame from John Hughes' real-time interactive animation of Bernard Morin's eversion of the sphere realized on a Stardent graphics computer. (J. Hughes, Brown University.)
This image , the cuboctahedral sphere eversion, is a piece-wise linear realization of this classical sphere eversion homotopy due to Morin, Denner and Apéry. (F. Apéry, G. Francis, C. Hartman and G. Chappell, University of Illinois at Urbana-Champaign.)
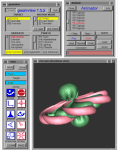
A frame from the film in progress ``Outside In,'' a sphere halfway through the Thurston eversion. In this example of a typical Geomview application, the Animator external module is being used to control a ``flipbook'' of the animation. The main ``geomview'' control panel at the upper left controls the viewing state, invokes modules, and brings up other control panels for control of lighting, object appearance, and so on. The basic mouse driven motion controls for changing the user's view are in the ``Tools'' panel on the left. (Geometry Center.)