Refraction of Light
To further our understanding of light and the rainbow, we now consider
what happens to light as it travels through water. This requires
relaxing our previous assumption that light travels at a constant
speed. It is known that the speed of light traveling through water is
less than the speed of light through air.
Note that Fermat's Principle would still hold if the mirror in Figure 1 were completely submerged in water.
Consider, then, what happens to the path of a light ray when a portion
of the light path is in the water and a portion in the air. In Figure
3, a light ray leaves point A and passes through B.
Instead of a mirror, consider what happens as the light ray passes
from air into water. Now, the air/water interface, like the mirror,
occurs at the point O. Recall that Fermat's Principle states
that light follows a path that minimizes total travel
time---regardless of the speed of the light ray. Therefore, unlike
our investigation with the mirror, our analysis of where the point
O occurs must consider both the speed of light in the air and
in the water.
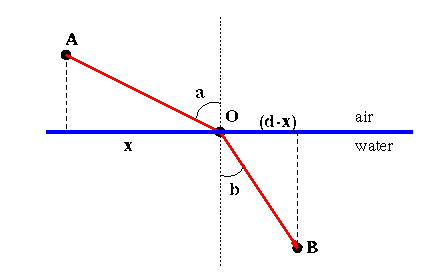
Figure 3: A light ray passing from air into water.
Question 2
Let c_a
be the speed of light in air and c_w the
speed of light in water. Remembering that distance equals speed times time,
- Write down the equation that x will satisfy if light minimizes
the time from A to B.
- Use this to derive an equation relating the sines of the angles
a and b to the speeds c_w
and c_a.
Referring to Figure 3 the angle that the path AO makes with the line
perpendicular to the water's surface is called the angle of incidence
and is represented by the angle a. The corresponding angle between
the path OB and the perpendicular is called the
angle of refraction and is represented by the angle b.
In Questions 2 you deduced Snell's Law or the
Law of Refraction which states that the ratio of the
sine of the angle of incidence to the sine of the angle of refraction is
a constant.
The speed of light in air depends on the temperature and pressure of the
air, and similarly for water and other substances. By contrast the speed
of light in a vacuum is an absolute constant, which we represent by
c.
The index of refraction for substances is the ratio
c/v where v is the speed of light in that substance.
Tables have been compiled for the ratio of the
speed of light in a vacuum to that of various other substances.
Question 3
Note that the Law of Reflection and Snell's Law
do not depend on the direction of the light ray. That is, our results
would have been identical if we had assumed that the source of
light was the point B instead of A. With this observation,
answer the following questions:
- If a medium has a large index of refraction, what does that say
about the speed of light in that medium?
- If light travels from one medium to another of
higher refractive index, what can you say about the way the light ray
bends in relation to the perpendicular (or the "normal"), to the surface
between the media?
- What happens when light travels to a medium
of lower refractive index?
Question 4
Experimentally it may be difficult to measure
the angle of refraction for a crystal with an unknown index of refraction.
- Given a "slab" of crystal of thickness T, draw a diagram
that depicts the passage of light through the crystal.
- What is the relationship between the angle of incidence and the angle
at which the light ray leaves the crystal?
- Design a method to experimentally
determine the angle of refraction in the crystal.
Question 5
Suppose we experimentally determine the index
of refraction for some crystal by accurately measuring the angle of
refraction, b0, that occurs when incoming light travels through a
vacuum and strikes the crystal at an angle of incidence equal to a0.
- Suppose now we slightly change the direction of the oncoming light
so that the angle of
incidence is now a=a0+da. Estimate
the new angle of refraction, b. Hints:
- Think of b as a function of a
and use your knowledge of calculus to write down
an approximation to b(a0+da).
Your answer should involve the quantity b'(a0).
- Compute b' by implicitly differentiating
an equation that relates b and a.
- Your final answer will be in terms of a0,
da, b0 and the index of refraction
of the crystal.
- Use the above to estimate the angle of refraction when
a0=45 degrees, da=5 degrees, and the crystal is
diamond. (You will need to look up the index of refraction for
diamond in a table.)
- Compute the actual angle of refraction for diamond for a 50 degree
angle of incidence. How close was your estimate to the actual
answer?
- Repeat the previous two questions for da=20 degrees. Is your
estimate better or worse in the case? Why?
Next: Rainbows: Exploration
Previous: How does light travel?
Return to: Outline
Frederick J. Wicklin <fjw@geom.umn.edu>
Paul Edelman <edelman@math.umn.edu>
This lab is based on a module developed by Steven Janke and published
in Modules in Undergraduate Mathematics and its Applications, 1992.
Last modified: Tue Oct 24 15:00:24 1995

