Boundary Conditions

It is a general mathematical principle that the number of boundary conditions necessary to determine a solution to a differential equation matches the order of the differential equation. The static beam equation is fourth-order (it has a fourth derivative), so each mechanism for supporting the beam should give rise to four boundary conditions.

Cantilevered Beams

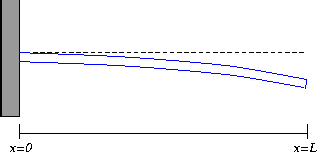
Figure 5: A cantilevered beam.

For a cantilevered beam, the boundary conditions are as follows:

w(0)=0 . This boundary condition says that the base of the beam (at the wall) does not experience any deflection.
w'(0)=0 . We also assume that the beam at the wall is horizontal, so that the derivative of the deflection function is zero at that point.
w''(L)=0 . This boundary condition models the assumption that there is no bending moment at the free end of the cantilever.
w'''(L)=0 . This boundary condition models the assumption that there is no shearing force acting at the free end of the beam.

If a concentrated force is applied to the free end of the beam (for example, a weight of mass m is hung on the free end), then this induces a shear on the end of the beam. Consequently, the the fourth boundary condition is no longer valid, and is typically replaced by the condition

w'''(L)= -mg

where g is the acceleration due to gravity (approximately 9.8 m/s^²). We note that we could actually use this boundary condition all the time, since if m=0 , it reduces to the previous case.

Simply-Supported Beams

Figure 6: A simply-supported beam.

A simply-supported beam (or a simple beam , for short), has the following boundary conditions:

w(0)=0 . Because the beam is pinned to its support, the beam cannot experience deflection at the left-hand support.
w(L)=0 . The beam is also pinned at the right-hand support.
w''(0)=0 . As for the cantilevered beam, this boundary condition says that the beam is free to rotate and does not experience any torque. In real life, there is usually a small torque due to friction between the beam and its pin, but if the pin is well-greased, this torque may be ignored.
w''(L)=0 . In the same way, the beam does not experience and bending moments on its right-hand attachment.

Question 7

A simply-supported beam of length L is deflected by a uniform load of intensity q . We assume that we know E, I, L and q . Let's use this fact to solve for the deflection of the beam under the load.

Integrate the static beam equation twice. (And please, please, please, remember the constants of integration!)
You now have an equation for w'' that depends on two arbitrary constants. Use two of the boundary conditions to solve for the two constants in terms of properties of the beam and load. (Cross off the boundary conditions that you use.)
The constants are now expressed in terms of known quantities, so substitute back into the equation for w'' and integrate two more times to get an equation for w .
Use the remaining boundary conditions to solve for the constants of integration in terms of known quantities.
Graph the deflection function (or -w if you want your beam to sag down) over the interval [0,L] to see if your equation makes sense.
For what position does the beam experience its maximum deflection? Where does the beam experience the most torque (the largest bending moment)? Where does the beam experience the greatest shearing force? Interpret your answers in terms of the physical meanings of these quantities.

Other Beam Supports

There are many other mechanisms for supporting beams. For example, both ends of the beam may be clamped to a wall. Or one end may be bolted and the other end is free to rotate. Or the beam may be clamped at one end but "overhang" a support placed at some point along its length.

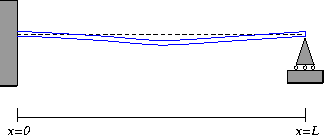
Figure 7: Other mechanisms for supporting beams.

Question 8

Each support mechanisms has an associated set of boundary conditions. In order to gain some intuition for boundary conditions, sketch idealized beams whose support mechanism gives rise to the following boundary conditions. The beams should be shown in a "deflected" position, as shown in the figures on this page. In all cases, the beam is supported only at the ends.

w(0)=0, w(L)=0, w'(0)=0, w'(L)=0 ; (This is called a doubly-clamped beam. Explain why.)
w(0)=0, w(L)=0, w'(0)= 0.2, w'(L)= -0.2 ;
w(0)=0, w(L)=0, w'(L)= 0, w''(0)= 0 ;
w(0)=0, w'(0)= 0, w''(L)=0, w'''(L)= -0.5 . (Hint: assume a cable is connected to the end of the beam at x=L .
Choose one of the above boundary conditions and find the deflection function for a uniformly distributed load of intensity q . Analyze the deflection function to determine the location of maximum deflection and maximum bending moment.

Next: Exploring Static Deformations of Beams
Return to: Modeling Deflections in Beams
Up: Outline

The Geometry Center Calculus Development Team