Next: Iteration
Up: Table of Contents
Prev: Introduction
MODULE: Dynamical Systems.
Part 2: Parametrized Families and Periodic Points
Parametrized Families
So far, the discussion has been about functions and the behavior of
orbits under iteration. In fact, in this lab, we do not study one
function, but a whole parametrized family of functions. That is, we
look at a whole series of related functions at once, and try to
understand how the eventual behavior under iteration changes as the
function changes. For example, in the introduction, you considered
the function f(x)=x^2. This is just one function within the
parametrized family f_c(x)=x^2+c. This family of maps is called the
quadratic family.
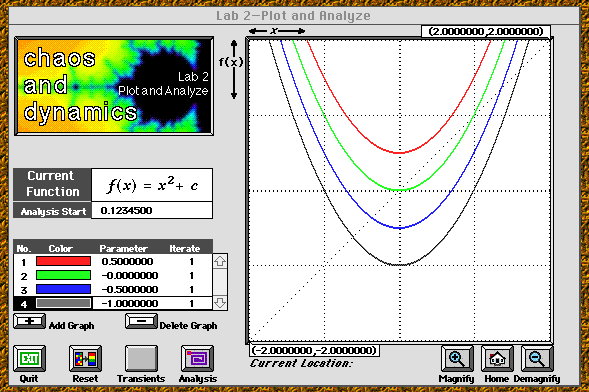
This picture shows the setup of Chaos Lab #2, along with maps from the
quadratic family for four different values of the parameter c.
- In the Chaos Lab #2, under the Function menu, choose the
option Quadratic. Push the Add Graph button, marked with
a "+". You should see a function in the quadratic family: y^2+c.
- Change the parameter: Notice the number under the column marked
Parameter. This is the value of c. Edit this number. How does
the graph of the function change as you vary the parameter? (You could
have predicted this from your knowledge of graphing parabolas.)
- Try simultaneously graphing two maps from the quadratic
family. To do this, hit the Add Graph (+) button twice and
change the values in the Parameter column.
- Choose another family off the Function menu. Notice the
equation for the graph you see. Try changing the parameter. Could you
have guessed how the graph of the function changed as you varied the
parameter?
Fixed Points
Remember that p is a fixed point for g if g(p)=p. Here is an
observation that makes it easy to find fixed points visually: every
point of the identity function i(x)=x is a fixed point. Therefore if
g(p)=i(p), then p is a fixed point. Fixed points are located where the
graph of g intersects the graph of i. Notice that the dotted diagonal
line in the graph window is actually the graph of the identity
function.
- Algebraically verify that 0 and 1 are fixed points of the square
root function and the squaring function. Verify that +1 and -1 are
fixed points of the function f(x)=1/x. Verify that 0 is a fixed point
of the "+/-" function.
- Verify that the quadratic family f(x)=x^2+c has fixed points of
the form
.5 (1+ sqrt(1-4c)) and .5(1-sqrt(1-4c)).
- For a variety of values of c, compare the graphs of functions in
the quadratic family to the identity map. Use this to determine where
these functions have fixed points. For each c, how many fixed points
are there? Are there the same number of fixed points for every c?
Relate your findings to the previous problem.
- Look at another family of functions by making another choice from the
Function menu. Determine where functions in this family have fixed
points. How many fixed points are there?
Periodic Points
Denote the nth iterate of g by g^n. For example, g^2(x)=g(g(x))= the
second iterate of x.
Definition: For a function g(x), a point p is periodic with
least period n if g^k(p)=p for k=n, and this is not true for any
smaller value of k. The orbit of p consists of only n points, since
g^n(p)=p. Since saying "least period" all the time is cumbersome, if
it is clear from the context, whenever we refer to a period n point,
it is assumed to be least period n.
- What is the period of a point under application of the "1/x"
button? What about the "+/-" button?
- Check that for g(x)=x^2-1, points (1+ square root(5))/2 and
(1-square root(5))/2 are fixed points. Check that 0 and -1 are
period two points.
The method of finding fixed points graphically also works to find
periodic points. For example, to find the points of least period two
for function g, look for points of intersection of the graphs of i and
g^2. The only catch is that fixed points are also period two points,
but not of least period two. Thus you must first find the fixed points
for g and discard them when looking at intersections of the graphs of
i and g^2.
- Use Chaos Lab #2 to graph the second iterate of the quadratic
family. To do this, change the value in the Iterate column from
1 to 2. For parameter c=-1, check graphically the number of points of
least period two. You may wish to simultaneously graph the first and
second iterates to see which points are least period two. Does
this agree with what you found above analytically?
- Graphically determine the number of period two points for
functions in the quadratic family at c=-0.4, -1.1, and -1.3? Remember
to exclude fixed points when you count intersections.
Just as with fixed points, periodic orbits can be attracting,
repelling, or neutral. For a given periodic orbit, if orbits of nearby
points converge to the periodic orbit, it is attracting. If orbits of
nearby points move away from the periodic orbit, it is
repelling. Otherwise it is neutral.
Next: Iteration
Up: Table of Contents
Prev: Introduction
![[HOME]](/pix/home.gif)
The Geometry Center Home Page
Author: Evelyn Sander
Comments to:
webmaster@geom.umn.edu
Created: Jun 09 1996 ---
Last modified: Jul 31 1996