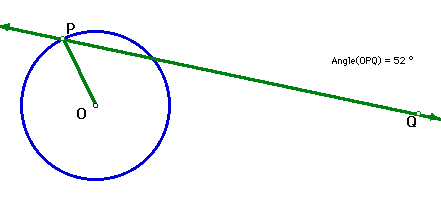
Using SketchPad, construct a circle, construct a point on it, and a line through this point. Drag the line around, until it appears to become tangent to the circle. Is there a special relationship between the line and the circle? Now draw the segment joining the center of the circle and the point on it. What angle do the two lines seem to form? Measure it using the "measure angle" feature. Is this angle special for the tangent line?

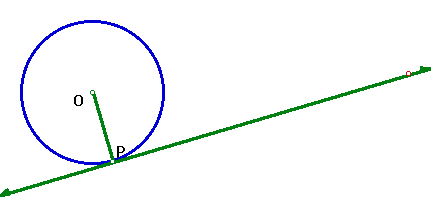
How can we use the previous property to construct a tangent line to a circle? Construct a circle, a point on it, and construct the tangent line at that point.
This is all good, but still we don't have a way of constructing a tangent line passing through a point outside the circle. We would know how to do it, once we find which point on the circle is the point of tangency. How do we find it? Look at what we know so far: the tangent line should be perpendicular to the radius, and it should pass through the given external point, Q, say. Let's look at all the lines satisfying these conditions.
Again, construct a circle, and a point Q not on it. Now construct a pair of lines: one through the center O of the circle, the other through the point Q, that are perpendicular to each other. Let P be the point of intersection of the two lines. Now move these lines around (by dragging point A, the point (other than O) defining one of the lines), and trace point P. What figure do you seem to get? Make a conjecture. Construct the figure, and check whether your conjecture was right or not.

Of all the possible positions of the points P, which one gives you a point of tangency? Is there more than one? How would you find it (them?) using the tools available in Sketchpad? And how would you then construct the tangent lines to a circle through an exterior point? Can you create a Sketchpad script of this procedure that can then be used again and again, with any circle and exterior point?
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Eduardo Tabacman, revised and edited by Evelyn Sander
Comments to:
webmaster@geom.umn.edu
Created: Jun 09 1996 ---
Last modified: Thu Aug 1 07:39:12 1996