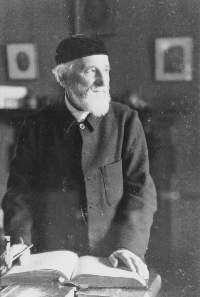
From Flatland to Hypergraphics: Interacting with Higher Dimensions
Department of Mathematics, Brown University, Providence, Rhode Island, USA
Flatland is over one hundred years old, and it has never been more popular than it is now, with five new English editions in the past six years, and translations into eight foreign languages. Much of its social satire is still pertinent today, and it is only now with the advent of modern computer graphics that we can begin to appreciate the challenge of seeing phenomena from higher dimensions which so baffled the two-dimensional protagonist of Edwin Abbott Abbott's little masterpiece. In this review we begin to answer the questions: "Who was the author of this book?" and, "How did he come to write it?"
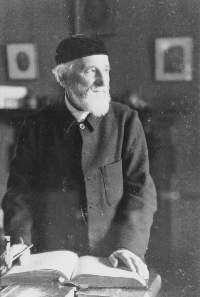
Just over one hundred years ago, a busy headmaster produced a slender book which was at the same time a satire on the self-limitation of social perspective in Victorian England and an introduction to the geometry of higher dimensions. This book, Flatland, has undergone several periods of popularity, including our present day, when five new editions have appeared in as many years and when several authors have written new books with Flatland as their inspiration. We may ask why the book has maintained its popularity over more than a century, and why its message about the fourth and higher dimensions has special appeal today. The answer relates to the concept of interacting with higher dimensions.
Edwin Abbott Abbott was not the first person to posit a two-dimensional universe inhabited by flat beings, but he was the first to explore what it would mean for such individuals to interact with phenomena from a dimension higher than their own. Today the development of high-speed computer graphics puts us face to face with such higher-dimensional phenomena, and in our investigations we are all too often just as ill-equipped to understand them as was 'A Square', the two-dimensional protagonist of Flatland, more than one hundred years ago. In this review we will trace some of the background and development of the dimensional analogy leading to Flatland. At the end we will indicate briefly how modern computer graphics is providing new meaning to its enduring message.
How did Flatland come to be written in the first place? Its creator. Edwin Abbott Abbott (Figure 1), born one hundred and fifty-two years ago, was a prolific author who produced over forty-five books in his fifty-year writing career, but he was not a mathematician. With the exception of a short passage on geometry in his book for tutors, governesses and parents entitled Hints on Home Teaching, he wrote nothing about mathematics besides Flatland, his nearly flawless introduction to the method of analogy in the treatment of different dimensions. It is something of a phenomenon for anyone, even an erudite Victorian headmaster (Figure 2), to write one hundred pages of anything geometrical without falling into all sorts of error or lapsing into outright nonsense. Abbott managed to avoid all these pitfalls even though his training and the majority of his writings were in the fields of classics, theology and history. Where did Abbott get his idea of using the dimensional analogy as the basis of his satire? How did he develop these ideas without falling into error? And how do these ideas fit in with the rest of Abbott's writing?
Figure 2. The City of London School in 1882, when Abbott was its headmaster.
It is difficult to summarize the life work of a man as broad as Abbott, but one theme emerges which unifies most of his efforts. He was concerned primarily with miracles and illusions, which in a very real sense he considered to be the same thing. We cannot know the Transcendental directly, and if ever we do receive glimpses of this realm, we will not be able to communicate our insights clearly. Yet we must try, using all the imperfect means of communication at our disposal even though we risk being misunderstood, rejected, and finally persecuted. This is the central lesson of the Gospels, and Abbott was a theologian who cared about the way the Gospels were received, in their own day and in his day.
Although the links cannot be drawn with certainty, we can identify several possible sources for Abbott's first encounter with higher-dimensional ideas. On the other hand, we can certainly identify what must have been the proximate occasion for Abbott to use these ideas in Flatland, in his contact with another Victorian writer, Charles Howard Hinton.
Background for the dimensional analogy
Before we can establish the connection between these two men, it is appropriate to set the stage for the development of the dimensional analogy. Before the middle of the 19th century, there was little speculation on the nature of the fourth or higher dimensions, in England or anywhere else; there was, however, a great deal of interest, both scientific and pseudo-scientific, primarily in England and in Germany. Several writers recognized the fundamental role of the fundamental analogy which became the basis of their expositions: just as we ascend from plane geometry to solid geometry, it is possible to continue and consider a subject beyond solid geometry. To appreciate the difficulties of understanding such higher geometries, it is useful to imagine the situation of a creature from a lower dimension attempting to come to terms with the third dimension. This `thought exercise' captured the imaginations of many different writers.
Fechner, Plato, and shadow figures
The first person to develop the dimensional analogy in the 19th century was the psychologist and physiologist Gustave Fechner in Leipzig. He wrote a small story, Space has Four Dimensions, as part of his collection Vier Paradoxe published in 1846 under the pseudonym of Dr. Mises. Fechner's two-dimensional creature was a shadow man projected to a vertical screen by an opaque projector. He could interact with other shadows, but, based on his limited experience, he could not conceive of a direction perpendicular to his screen. Fechner suggests that for such a being, time would be a third dimension, expressing the movement of his whole screen in a direction which he cannot comprehend spatially. The idea of treating shadow figures goes back much further, to Plato's Allegory of the Cave in the seventh book of The Republic. There the shadows are merely representations of objects to be viewed by three-dimensional observers who are artificially limited to seeing only these lower-dimensional views. Plato does not suggest that the shadows have the capability of interacting with one another, and this is the heart of Fechner's insight.
Helmholz and non-Euclidean geometry
Fechner's story about a two-dimensional man was reprinted in his Kleine Schriften in 1875, and his ideas were referred to in the British journalMind in 1876 when J. M. P. Land responded to an article by a colleague of Fechner, Hermann von Helmholz. In the mid-19th century, there was considerable interest in non-Euclidean geometry, and when he wrote about that subject, Helmholz employed the device of imagining the difficulty of a two-dimensional creature constrained to move along some marble surface, trying to come to a knowledge of the intrinsic geometry of his world without the benefit of a three-dimensional perspective that could reveal its curvature properties all at once. An English version of his work had appeared in Academy as early as 1870, and the extended article was developed in Mind under the title The Axioms of Geometry.
Gauss, Riemann and intrinsic geometry
Interest in the intrinsic geometry of surfaces can be traced to the work of Gauss, who in his 1827 Treatise on the Geometry of Curved Surfaces encouraged his readers to imagine the sorts of measurements that would be made by intelligent flatworms moving along the surface of a membrane in space. His concern with geodesy led him to recognize the effect of curvature on geometry, for example in determining the sum of the angles of a triangle drawn with shortest lines on a sphere or an irregular surface. These ideas were elaborated in 1854 in the dissertation of Bernhard Riemann, The Hypotheses Which Underlie Geometry, which introduced intrinsic measurements on abstract spaces of any number of dimensions and did not require reference to a containing space of higher dimension in which material objects were supposed to be 'curved'.
All these ideas were familiar to mathematicians in England, and they began to reach more popular audiences through the efforts of Helmholz and the British scientist John Tyndall who had met Helmholz in Germany in 1854. (It may be mere coincidence that Edwin Abbott Abbott was invited to tea at the home of George Eliot and Charles Lewes in 1871, on the same day that Tyndall came there for dinner. Lewes was himself very much caught up in the interpretation of Kant in relation to the geometry of higher dimensions, as is evidenced by the correspondence following a speech by J. L. Sylvester, A Plea for the Mathematician, which extolled the power of generalization of geometrical as well as algebraic ideas to higher dimensions.)
Figure 3. Abbott's own drawing of the house of 'A Square', which summarizes the social structure of Flatland. A Square's wife and daughter are drawn as single lines, and, in ascending social order, the male servants, butler, footman and page, are triangles. The owner is A Square, and as each future generation adds a further angle, the Square's sons are the four pentagons and his two grandsons the two hexagons. The entrance doors to the house are of an appropriate width for the two sexes.
Zöllner and the spiritualists
The most widespread interest in the fourth dimension was not among the scientists and mathematicians, however, but among the spiritualists who co-opted the idea to express their own theories. The American medium (and prestidigitator) Henry Slade had become famous when he was expelled from England for fraud connected with spirit writing on slates. There was therefore tremendous skepticism when he reappeared as the primary proof in the pseudo- scientific efforts of another colleague of Fechner and Helmholz in Leipzig, the astronomer J. P. F. Zöllner. Unlike Fechner and Helmholz, who maintained some semblance of respectability, Zöllner became almost completely discredited because of his association with spiritualism. He realized, quite correctly, that anyone with access to higher dimensions would be able to perform feats impossible for someone limited to only three dimensions. He suggested several experiments which would demonstrate his hypothesis, for example linking solid rings without first cutting them apart, or removing objects from secured boxes. Although Slade never quite performed the stated tasks, he always managed to come up with something similar enough to convince Zöllner, and these experiences became the primary basis of his Transcendental Physics. This work and the claims of other spiritualists were widely debated in the popular press as well as by some serious scientists.
Abbott, illusions and miracles
Abbott was certainly aware of these ideas although he did not express any interest in them. However, they must have represented some fascination to him on one level, since they raised from a different viewpoint one of his primary concerns, namely the relationship between illusion and miracle. If what we perceive as a miraculous event, contrary to the laws of nature, later appears as the quite natural manifestation of some reality we had not previously recognized, then we have to re-evaluate the whole situation in the light of the new knowledge. What had appeared to be contradictory and not worthy of belief or acceptance now becomes a set of new facts that can be reconciled with a larger body of knowledge. One lesson from this is that we should not be dependent on miracles as the basis for our beliefs, either in spiritualism or in conventional religions.
Garnett, Maxwell, and physics
Another tie-in between Abbott and the scientific establishment came through one of his students, William Garnett, who was first boy in mathematics at the City of London School in the same year that H. H. Asquith, the future prime minister, was first boy in classics. Garnett went to Trinity College in Cambridge and became the chief assistant of the eminent physicist James Clerk Maxwell. He collaborated with Lewis Campbell on Maxwell's biography. That book shows Maxwell's continued interest in higher dimensions, in his correspondence and in his verse, where he referred to the fourth dimension as the place where knots could be untied:
My soul is an entangled knot Upon a liquid vortex wrought The secret of its untying In four-dimensional space is lying.
Garnett remained in contact with Abbott throughout his career, so it is quite likely that he would have shared his ideas with him once he realized that Abbott was interested in this kind of geometry. After his retirement, Garnett moved to Hampstead, where Abbott was living. He signed Abbott's eightieth birthday message and was present at his funeral in 1926. He was the obvious choice to write the introduction to Flatland when that book was republished in the same year by Basil Blackwell. In his lead paragraph, he chose a verse Maxwell had written for the Cayley Portrait Fund, describing the futility of trying to capture on the surface of a two-dimensional painting the soul of someone `who in n dimensions flourished unrestricted'. He also cited a letter in Nature six years earlier referring to Abbott as a prophet who foresaw the relevance of the dimensional analogy for understanding the passage of time in relation to space. That letter was signed `W.G.', and if we need any additional evidence that it was written by Garnett himself, we can point to the appearance in the Flatland introduction of the relatively unusual phrase jeu d'esprit, used twice by Garnett in his Maxwell biography published in that same year, 1926.
Hinton and Candler, the Uppingham connection
Was any of these possible sources the particular place where Abbott first learned about the idea of the fourth dimension? Whatever the first contact might have been, we can almost certainly discover the primary association that led Abbott to take up this idea as the basis of his combination of social satire and philosophical exercise, namely his encounter with the work of Charles Howard Hinton.
Hinton was 15 years younger than Abbott, educated in mathematics at Oxford, and interested in physical science and a non-traditional philosophy related to the ideas of his father James Hinton, a colleague of Havelock Ellis. Hinton had already written an article on the fourth dimension in 1880, published in the University of Dublin Magazine and reprinted in the Cheltenham Ladies' Gazette in 1881. He was teaching at Cheltenham Ladies' College at the time and Abbott was quite closely connected to women's educational issues which brought him into contact with the headmistress of that school, Miss Buss. It is possible that he first encountered Hinton's work through one of these publications. More likely, however, is an encounter between these two men in person after Hinton became science master at the Uppingham School, where the mathematics master was Abbott's lifelong friend Howard Candler.
Candler and Abbott had met when they were both schoolboys at the City of London School. They went up to Cambridge together and stayed in contact for the rest of their lives. During the 25 years Candler was at Uppingham, they exchanged letters every week. (Abbott's letters to Candler were extant as late as 1939, when they were used as a source in writing the history of the City of London School, but they have since disappeared.)
After his retirement, Candler moved to Hampstead so he and his family could be close to the Abbotts. Abbott consistently consulted Candler about his theological writings, so it is virtually certain that he would have written to him about the geometrical part of Hints on Home Teaching. And Abbott would certainly share with Candler his thoughts on Flatland, which bears the dedication 'To the Inhabitants of Space in General and H.C. in particular'. Abbott specifically identifies Candler as 'the H.C. to whom Flatland wasdedicated' in the introduction to one of his theology volumes written just after Candler died in 1916, and the first edition in the Trinity College library, donated by one of Candler's grandsons, is inscribed simply 'To H.C., in particular'. It is easy to imagine a series of letters in which Candler mentions to his friend the ideas of this new science master, Hinton, and their relevance to some of the theological and philosophical notions which they have been discussing. Exactly when the idea of writing a social satire took shape would be difficult to tell, but it almost certainly was written in the middle of the year 1884 and was published that fall. Did Hinton and Abbott ever meet? There is no absolute evidence of this, but it is very probable since the Abbott family frequently traveled to Uppingham to meet the Candlers and it is likely that Abbott would have known his friend's colleagues. Abbott certainly knew the Uppingham Head Master Edward Thring, who founded the Head Master's Conference, for which Abbott served as secretary. Unfortunately, Thring had to dismiss Hinton after he had confessed the crime of bigamy. Candler is not mentioned in the portion of Thring's diary in which Hinton's unfortunate story is chronicled. Hinton left England and eventually came to America where he continued his work on the physics and philosophy of the fourth dimension. It is unlikely that he and Abbott had any further contact. The appearance of Abbott's Flatland did not prevent Hinton from using the same place name the next year in his An Episode of Flatland, and one must wonder about the possible strain on relationships which must have ensued. Apparently, however, the situation was not viewed as hostile by the two authors themselves. Each refers to the other in later works which indicate that they saw their efforts as complementary rather than competitive.
The key reference from Abbott's side is in his 1887 book The Kernel and the Husk. In discussing spirits he writes: "You know - or might know if you would read a little book recently published called Flatland, and still better, if you would study a very able and original work by Mr C. H. Hinton - that a being of Four Dimensions, if such there were could come into our closed rooms without opening door or window, nay could even penetrate into, and inhabit our bodies..... Even if we could conceive of Space of Four Dimensions - which we cannot do although we can perhaps describe what some of its phenomena would be if it existed - we should not be a whit better morally or spiritually. It seems to me rather a moral than an intellectual process, to approximate to the conception of a spirit: and toward this no knowledge of Quadridimensional space can guide us."
For his part, Hinton replies in Scientific Romances, first published in 1888, including an essay `What is the Fourth Dimension?' and ending with three papers on higher dimensions. As an introduction to this last collection he writes: "And I should have wished to be able to refer the reader altogether to that ingenious work, Flatland. But on turning over its pages again, I find that the author has used his rare talent for a purpose foreign to the intent of our work. For evidently the physical conditions of life on the plane have not been his main object. He has used them as a setting wherein to place his satire and his lessons. But we wish, in the first place, to know the physical facts."
Indeed the work of Hinton continues to concentrate on the technological aspects of two dimensions and higher. After coming to the United States and teaching at Princeton and at the University of Minnesota, he worked at the us Patent Office in Washington, DC, and wrote papers on physics and mathematics, often using the fourth dimension as an explanatory device. (The contemporary mathematician A. Dewdney, with his studies of two- dimensional technology, is the spiritual descendant of Hinton and the scientific realm. The philosophical side of Hinton is represented in our day by the logician and writer Rudolf Rucker, who has collected representative writings of Hinton under the title Speculations on the Fourth Dimension.)
Abbott and philosophy
But if Abbott was not primarily interested in the physical aspects of existence on a plane world, what was his object? He answers the question for himself in his book The Spirit on the Waters, written nearly ten years after Flatland and including the name of that book on the title page along with three others by the author: Philochristus, Onesimus, and The Kernel and the Husk, all of which were first published anonymously. In The Spirit on the Waters, he recounts the climactic visitation scene from Flatland where the hero, A Square, is confronted by the changing shapes produced in his two-dimensional universe by the passage of a being from the third dimension. He discusses the possible responses of the square, the most immediate of which might be to worship this being because of its mysterious God-like powers. Not so, says Abbott. Physical or intellectual powers do not automatically signify any of the moral and spiritual qualities we must demand of any object of our adoration. He concludes:
"This illustration from four dimensions, suggesting other illustrations derivable from mathematics, may serve a double purpose in our present investigation. On the one hand it may lead us to vaster views of possible circumstances and existence; on the other hand it may teach us that the conception of such possibilities cannot, by any direct path, bring us closer to God. Mathematics may help us to measure and weigh the planets, to discover the materials of which they are composed, to extract light and warmth from the motion of water and to dominate the material universe; but even if by these means we could mount up to Mars or hold converse with the inhabitants of Jupiter or Saturn, we should be no nearer to the divine throne, except so far as these new experiences might develop in our modesty, respect for facts, a deeper reverence for order and harmony, and a mind more open to new observations and to fresh inferences from old truths."
That last sentence just enlarges on the final phrase of Flatland's dedication, hoping that the experience of the dimensional exploration will contribute 'To the Enlargement of the Imagination and the Possible Development of that most rare and excellent gift of Modesty Among the Superior Races of Solid Humanity'.
Flatland and theological fiction
We have identified any number of sources from which Abbott could have learned about this notion of the fourth dimension. But he seems to have been the first to have developed it into a social allegory and the first to treat the possibility of an encounter between beings of different dimensions, with all its challenges and frustrations. Abbott was quite conscious of the limitations imposed by Victorians on their own ways of thinking and knowing. He saw the most important message, the word of Christ, being dismissed by his contemporaries because they could not accept the trappings of miracles which the Scripture writers used as the means of trying to communicate their story. He tried to separate the message from the miraculous language, one of the most ambitious projects of the Broad Church movement.
At one point he wrote a plea to George Eliot to take up the challenge of writing a novel to express the Gospel message free of miraculous language. She did not do so and ultimately Abbott himself completed Philochristus and Onesimus, each of which told a similar story, one that would later appear in more graphical form in Flatland. In Philochristus, the protagonist is a Pharisee in the early first century, and Onesimus is the story of the Greek slave in St. Paul's Epistle to Philemon. In each case the storyteller finds himself in a society which provides all the answers within a certain limited perspective. The story sets forth circumstances which do not fall precisely into the framework of the societal system, thereby requiring a higher principle of explanation. Then comes the climactic encounter with a figure totally out of the ordinary, in one case Christ himself and in the other St. Paul. The hero is totally transformed by the revelation of a higher order of being and ultimately returns to his home society to try to spread this good news, only to face frustration and eventual persecution.
It is easy to see where Flatland fits into the context of Abbott's lifelong project. This one small volume gives him a chance to examine just that much more closely the limitations of Victorian society, its preoccupations with class consciousness, social Darwinism, resistance to the rights of women or minorities or misfits, and a growing two-cultures mentality separating the rational from the intuitive and the theoretical from the practical order. The tradition of satire established by Swift is present, attacking some of the same blindness Gulliver met in Laputa or which Alice ran into in another more recent allegory. Flatland is different, however. It is Gulliver's TravelsAlice in Wonderland from the viewpoint of the White Rabbit. We do not enter into a strange world ourselves. A strange world surrounds us, and we have to deal with it.
It is curious in a way that Abbott did not choose to write a play. His specialty in literature was Shakespeare and quotes from the plays head each of the chapters of Flatland. Several are mere plays on words, but the key passages indicate Abbott's favorite, considering the theme at hand, namely The Tempest: 'O Brave New World(s) that have such people in 'em.' When we encounter new worlds we share Miranda's wonder, to be sure. Vainly we struggle to preserve the order we already know, and finally we let go and give ourselves over to the new insight, wherever it will lead us, knowing that our experiences will never look the same again.
Conclusion
Abbott's career as teacher, writer, scholar, and keen observer of his world all prepared him for an examination of society and theology which would break bonds and help people react in new ways. Victorian England has been described as an age of transition. Flatland comes at a transition time for its age and for its author. It summarizes the more than twenty books Abbott had written before and sets the stage for the other half of his considerable production of writing on so many topics. It still seems odd that of so many works which seemed of greater moment, the piece that survives and secures Abbott's immortality is probably the one he most enjoyed writing. It came in a remarkable era, a key document in the life of a remarkable man. We who have had our imaginations enlarged and our modesty challenged can only be grateful.
Visualizing higher dimensions today
What Abbott and other 19th-century writers envisioned has become a reality in our present day. Encounters with phenomena from the fourth and higher dimensions were the fabric of fantasy and occultism. People (other than the spiritualists) did not expect to see manifestations of four-dimensional forms any more than they expected to encounter Lilliputians or Mad Hatters. Today, however, we do have the opportunity not only to observe phenomena in four and higher dimensions, but we can also interact with them. The medium for such interaction is computer graphics. Computer graphic devices produce images on two-dimensional screens. Each point on the screen has two real numbers as coordinates, and the computer stores the locations of points and lists of pairs of points which are to be connected by line segments or more complicated curves. In this way a diagram of great complexity can be developed on the screen and saved for later viewing or further manipulation (Figures 4 and 5).
Figure 4. Projections of orbits from the hypersphere into three-dimensional space.
For use in architecture or engineering design, the computer must encode information about points in three-dimensional space, with each point specified by a triple of real numbers. The computer can then display any two- dimensional view of the object, not only the traditional front, top, and side views, but pictures from any chosen viewpoint in space. The technical device which accomplishes this is a rotation matrix, which keeps track of what happens to a given reference frame. Once we tell what happens to the segments in the reference frame, the positions of the rest of the points are determined in a straightforward manner and projected on the two-dimensional screen. Although we only see two of the coordinates, the third is kept in the computer, ready for further explorations.
Unlike its human operator, a computer has few preconceptions about what dimension it is in. Just as easily as it keeps track of three coordinates for each point, it can, when properly programmed, keep track of four or more coordinates. Often a fourth coordinate can indicate some property of the point on the screen, like color or brightness. At other times it can represent a fourth spatial coordinate, interchangeable with the other three, just as the length, width, and height of a box can be manipulated in three-space. If we want to work with a four-dimensional box, we must provide information of a reference frame with four segments, not just three. In the same way that we can complete a drawing of a three- dimensional box once we know the images of the three segments in a reference frame at one corner, we can make a three-dimensional model of the shadow of a four-dimensional box once we know the positions in three-space of the images of the four segments in a four-dimensional reference frame. We can then go further and project this three-dimensional framework down to the computer graphics screen, where we can interact with it the way we did with the blueprints for a building or the plans for a machine tool. Thus we use all of our experience with interpreting two- dimensional images of three-dimensional objects to help us move up one further step to interpret the three-dimensional representations of objects which require a fourth coordinate for their effective description.
Figure 5. Hypertorus projected from four-dimensional space, half- way to infinity. (Both Figures 4 and 5 are from T. F. Banchoff, Discovering the Fourth Dimension, Prime Computer Inc., Natick, Massachusetts, USA, 1987.)
But what kinds of phenomena call for such higher dimensional analysis? In addition to the natural extensions of abstract plane and solid geometry to a fourth and higher level, there are intensely practical applications of any facility we may achieve for visualizing phenomena in four and higher dimensions. One of the most significant is the field of exploratory data analysis. A simple table showing the correlation between height and weight of a number of individuals in a city is easier to interpret when the data are presented in a scatterplot, where information about each person is represented by a point in two-dimensional coordinate system. If the points tend to cluster around a line, then there is a trend which can be expressed in a simple linear equation, which can help to predict facts about further data.
If the table contains a third number for each individual, say shoe size, then the scatterplot requires three dimensions. Again a trend might be observable if the points are situated near some particular line, or some plane. Standard techniques in statistics can help to identify such linear relationships even before there is any recourse to a three-dimensional scatterplot. Of course a computer could produce such plots by projecting the points from three-space down to various planes to try to find especially revealing views.
This technique is usable for much more complex phenomena, where the characteristics of each individual might be described by four, five, or more variables. It is easy to imagine data sets from economics or biology or physics where each data point might have dozens or hundreds of coordinates. Exploratory data analysis provides a way for human observers to interact with such high- dimensional data sets, studying collections of views obtained by projecting the data down into two- or three-dimensional spaces. It may be that various configurations of data resemble configurations already observed by studying images of model structures, not just lines and planes but also more complicated curves and surfaces. Our experience with the phenomena of geometry of curves and surfaces in three- and four-dimensional space provides the tools for interpreting data configurations which arise from real-world observations.
We will never be able to comprehend the structure of a cloud of points in four-dimensional space in the same way that we take in a pattern of points on a plane or learn to understand the intricacies of a framework in ordinary three-space. We share with A Square, the protagonist of Flatland, an inability to 'see' in a dimension higher than our own. But, like A Square, we can develop ways of responding to the representations of higher-dimensional phenomena in our world. The challenge of modern computer graphics fits right in with one of the chief aims of Edwin Abbott Abbott in the introduction of his timeless book, namely to encourage in the races of solid humanity that estimable and rare virtue of humility. We will continue to appreciate Flatland more and more in the years to come.
Figure Al. Title page of first edition (1884) of Flatland.
Appendix: Bibliographical History of Flatland
October 1884 Pre-publication issue distributed by the author.
November 1884 First edition of one thousand copies appears (Figure Al) and is reviewed in several magazines.
December 1884 Second, revised edition appears, with a new introduction by the author and several emendations in the illustrations and the text.
1885 American edition appears, based on the uncorrected first edition. Numerous editions follow for the next 55 years.
1886 Dutch translation appears, De Mijs Publishers.
1926 Basil Blackwell republishes the second edition, with an additional introduction by William Garnett. Numerous editions follow up to the present day.
1929 Abridged German translation appears, Teubner Verlag.
1952 Dover Publications, Inc., republishes the second edition, with a new introduction by Banesh Hoffmann. Continuously published to the present.
1963 Barnes and Noble edition, with Garnett introduction.
1966 Italian translation by Masolino D'Amico, Adelphi, Milano.
1968 French translation by Editions Deno‘l, Elisabeth Gille, translator, reprinted 1984.
1976 Russian translation, with notes by Yuri Danilov, Mir Publishers.
1976 Spanish translation, Ediciones Guadarrama, Madrid, translated by Jesus Villa.
1977 Japanese translation, Blue Backs.
1978 Grant Dahlstrom, Pasadena, California, with notes by David W. Davies.
1982 Arion Press edition, introduction by Ray Bradbury.
1982 Emerson Books, Inc., edition, introduction by Karen Feiden.
1982 Complete German translation, Klett-Cotta Press, Stuttgart, translated by Joachim Kalka.
1983 Barnes and Noble edition, introduction by Isaac Asimov.
1984 Hebrew translation, Keter Publishing House, Jerusalem.
1984 New American Library Signet edition, introduction by Alexander Keewatin Dewdney.
1988 Penguin Book edition, introduction by Banesh Hoffmann.
The manuscript was received 20 November 1989.