
Consider the graph of the identity function w = z. Here z = x + yi and w = u + vi where x, y, u, and v are real variables. We choose as the domain for z the unit square in the z-plane, given by -1 <= x <= 1, -1 <= y <= 1, so the ranges of u and v will also be given by the same interval. The graph of the identity function will then be a parallelogram in four-space with its four edges along the diagonals of four of the square faces of the hypercube.

In the same way, we can look at the graph of the squaring function w = z^2. We can approach this by finding the real coordinates of the points on the graph, first expanding the square of x + yi algebraically and then separating the resulting complex number into its real and imaginary parts: z^2 = (x + yi)^2 = x^2 + 2xyi + (yi)^2 = (x^2 - y^2) + (2xy)i = u + vi. Thus we can insert into our four-dimensional grid the points (x, y, x^2 - y^2, 2xyi) where (x,y) runs over the points of the unit square. We can then observe various views of that graph as we rotate the hypercube.

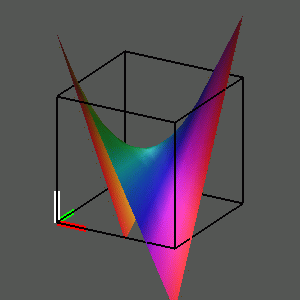
To observe this, play the movie
Unfortunately we observe that the graph of the squaring function does not stay "inside" the hypercube! To see why this is so, observe that the corner (1, 1) of the square is sent into ( 1, 1, 0, 2 ), and the other three corners are similarly sent to points with coordinates of absolute value greater than 1. We can decide to live with this, realizing that the distortions are going to be even greater for higher powers of z.
We summarize this investigation of the graph of the complex squaring function in rectangular coordinates by situating the two images at the vertices of a diagram, with arrows between the vertices. Selecting any vertex plays a movie of a rotation of that object in three- space, and selecting the arrow plays the rotation in four-space from one view to the other.