This particular implementation attempts to intelligently implement this basic strategy by
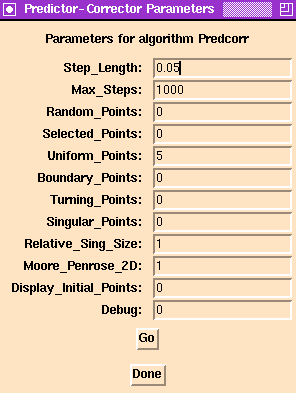
Step_Length in the direction tangent
to the curve, before using Newton's method to correct back onto the
curve. Due to this correction, the actual length of the line segments
outputted by the algorithm will vary somewhat at different points
along the curve. If Moore_Penrose_2D is off or if the model domain is of
dimension greater than 2, each segment will have length AT LEAST
Step_Length.The following parameters allow the user to choose among various methods of selecting initial points. At least one of these fields must be nonzero in order to obtain output. Several or all of them may be selected at once.
Moore_Penrose_2D is set to 1. See
documentation for Moore_Penrose_2D below.
Default value: 50
Uniform_Points in an
n-dimensional model, the algorithm constructs a uniform grid with m^n
points, and attempts to iterate each point onto the curve using
Newton's method. Specifically, the algorithm divides the domain space
into m^n uniform n-cubes, and places a grid point at the center of
each cube.Boundary_Points, the grid used is
uniform as described above, with m^(n-1) points per boundary. All
initial points found by this method will be along the boundaries.
WARNING: When using models with a large number (n) of dimensions, be
careful not to use large values (m) for Uniform_Points,
Boundary_Points, and Turning_Points.
The values in these fields do
not indicate the total number of seeds to use; they represent the
fineness of the grid. The functions which find uniform and turning
points use m^n seed points, while the one which calculates boundary
points uses m^(n-1) seed points per boundary. Large values of
Turning_Points (say, above 10 for three or more dimensions) may cause
the algorithm to be especially slow, since turning point iterations
are relatively complex and since a separate set of these iterations
must be executed for each coordinate axis for each point.
Singular_Points parameter specifies the fineness of the grid, as
described above under uniform points), and attempts to iterate each point onto a
singularity of the function. In general, we define a singularity as a
point where the Jacobian of f is rank deficient. Singularity
detection and handling is currently implemented only in 2 dimensions,
so setting this parameter to a nonzero value with a higher dimensional
model will cause an error message. In two dimensions, a singularity
is simply a point where f=0 and both partial derivatives of f are 0.
Singularity searches are based upon Newton's method, but are more
complicated than those described above -- both because the system is
overdetermined and because the search conditions degenerate as the
algorithm approaches a higher-order singularity, causing the search to
become unstable. We deal with the latter problem by using an algorithm based on an extension of ideas presented in a paper by W. Govaerts, which dynamically adds search conditions as it approaches a higher-order singularity. When a singularity is found by this routine, a region surrounding it is "desingularized." That is, a local approximation to the curve in this neighborhood is computed and drawn. The singularity point itself is not used as an initial point, but near-singularity points found at the boundary of the desingularization region are used. Singularity detection is generally slow compared to other methods of finding initial points. The above warning applies, even though n=2.
Relative_Sing_Size
times Step_Length. For a higher order singularity, the
desingularization region is a square centered at the singularity with
side length of twice the singular radius.
For a node, the singularity-handling
routines trace a distance equal to the singular radius in each
of the four tangent directions.
The 2D search methods also differ from the general ones
(when used for a planar model) in that they use a different variant of
Newton's method. These functions are called in cases when Newton's
method is in fact being used to solve a system which is
underdetermined by one equation. Classically, Newton's method
requires a fully determined system (i.e., it involves the inversion of
a square matrix). The general procedure solves this problem by
introducing the additional condition that the iterations occur within
a hyperplane perpendicular to a previously determined vector (the
vector used is typically a tangent vector; when stepping along the
curve, it is the vector indicating the direction in which the step was
taken). The "optimized" functions do not add this extra condition;
they implement Newton's method on an underdetermined system, using the
method of the Moore-Penrose inverse described in Allgower and Georg.
For the planar case, this simply involves recomputing the gradient at
each iteration, and taking a Newton's step in that direction. Our
experimentation shows that (after we fixed a seemingly endless string
of bugs in these optimized functions) the optimized functions tend to
give better results than their general counterparts, and to execute
slightly faster. However, the behavior of the optimized functions is
sometimes less predictable, and we have found a few cases where the
general functions gave better results.
Default value: 1
Debug is 1, a very large quantity of unimportant information will be
displayed on the standard output. This output describes whether or
not Newton's method successfully converged to each initial point, and
how the line segments were traced between the initial points. This
option is not intended for general use, although some people find the
debugging output strangely interesting.
There are also some graphical effects when Debug is set to 1.
After the algorithm computes all of its initial points, it selects an
appropriate subset of those initial points to be used in the tracing
of the curve. When both Display_Initial_Points and Debug are set to
1, the initial points that were NOT selected to be used to trace the
curve will also be displayed. Points that were too close to another
point will be displayed as blue dots, and points that were outside of
the bounding box will be displayed in green.
If you want your X server to spend minutes on end outputting
text debugging information, then try setting Debug to 2 (which will
output everything you get with Debug set to 1, and more).
Default Value: 0
You may also encounter one of the known output bugs. None of these bugs are intrinsic to the Predictor-Corrector algorithm; they are caused by the Pisces graphics code or by Geomview. Most of the glaring output bugs have been fixed, but a few remain. In particular, if you use Geomview as your output device, you will occasionally be informed that Geomview can't seek back far enough on its input pipe (and no image will be drawn).
Future improvements to predictor-corrector will include improved singularity detection and improved singularity handling (tracing within the desingularization region).
Please send bug reports to
software@geom.umn.edu.
The summer students were
![[Pisces]](../../../pix/pi.gif) The Pisces Home Page
The Pisces Home Page