Partial Solutions to Brainfood #1

1. No, we cannot tell where the image of t=0 is soley by looking at the curve. For example, the function q(t)=(cos(t+Pi), sin(t+Pi)) has EXACTLY the same image (the unit circle), but the point t=0 is sent to (-1,0) instead of to (1,0).
2. The vector c translates the image of the parametrized cicle by c.
3. No, you can't determine velocity vectors. The function r(t)=(cos(2t), sin(2t)) has the unit circle as its image, but it traces out the circle twice as fast as the function p, therefore the velocity vectors are twice as long.
4. c) The path is a helix.
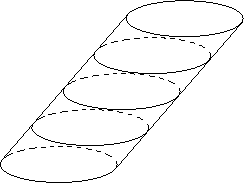
5. Stacking circles that are being linearly translated as they are stacked results in a "slanted cylinder" as shown below.