Partial Solutions to Brainfood #6

1. The function is f(x,y)=x^2-y^2+1. Note that f(0,0)=1 and that f restricted to the circle parametrized by C(t)=( 0.1 cos(t), 0.1 sin(t) ) is

   0.01 cos^2(t) - 0.01 sin^2(t) + 1.

   This function oscillates between 0.99 and 1.01, so sometimes it is greater than f(0,0) and sometimes it is less. This is indicative of the neighborhood of a saddle point: for a saddle point there will be two "sectors" of direction in which the function is less than the critical value, and two sectors of directions in which the function is greater than the critical value.

   If the critical point were a minimum, then we would expect the restriction of f to a small circle about the critical point to always be greater than the critical value.

2. a) Critical point at (1,-2). D=4. Maximum.

   b) No critical points.

   c) Critical point at (1,2). D=-5. Saddle

   d) Critical point at (0,0). D=0, so the test fails. Evaluating the function on a small circle shows that the critical point is a minimum.

   e)There are two critical points. The one at (0,0) is a saddle. The one at (2/3,-2/3) is a local maximum.

3. The purpose of this question is to get you to think about glocal features of surfaces. The best way to think about the problem is to sketch level sets of functions, and try to draw a level set that satisfies the friend's claim.

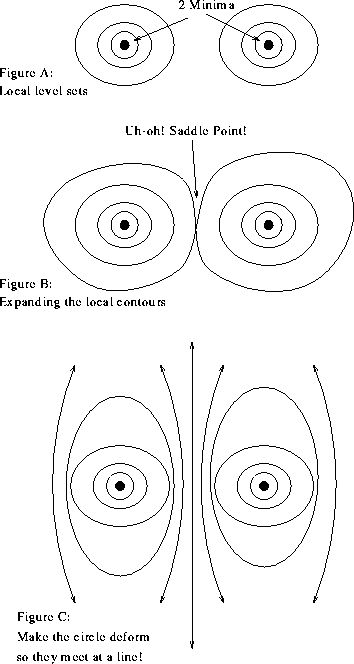
   One correct answer is that a function with exactly two isolated critical points, both minima, does exist! A sample answer is below (a good "partially correct" answer stops at Figure B). Notice, however, that the example function has an entire line of critical points, so it is also correct to draw Figure 3 and say "no, because there is a whole line of critical points.

   If you actually tried to write down a formula for such a function, you probably didn't get far. Formulas do exist, but you need to construct them by understanding the geometry of surfaces.

   ---

   A function exists that has two isolated critical points and no other isolated critical points. Here's what I did. I thought about contours (level sets) of a function that has only two minima. Near the minima, I know that the level sets look like little circles. (See Figure A.) As we move away from the critical points, the contours get bigger. At first I thought that the circles would have to touch, creating a saddle point (Figure B). But THEN I REALIZED, if make the circles get "flat" as they approach each other, then, in the limit, the circles will intersect on a LINE, and that's not the local topology of an isolated critical point. Note, however, that every point on the curve is a critical point, so I guess the question should have said "isolated critical points" in its statement. For the question as written, maybe the answer is "no"?