


Next: Plotting with Maple
Up: Maple for Vector
Previous: Basic Maple Syntax
The following commands are briefly summarized for your use. For further
information about any of these commands, as well as examples of their
usage, use the on-line Help Browser or type ?commandname.
Note: The plotting commands we will be using are described in the next
section.
- diff
- This command is used to compute the (partial) derivative of a
function.
To differentiate an expression f with respect to the variables x1, x2,
 , xn use
, xn use
diff(f, x1, x2, ..., xn);
For example, the derivative of 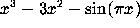 is
computed by
is
computed by
diff( x^3-3*x^2 - sin(Pi*x), x);
QUESTION 2: What is the derivative of 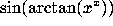 ?
?
- evalf
- This command is used to evaluate a symbolic expression
numerically to n digits accuracy.
evalf(expr, n);
For example, evalf( 1 + (Pi/12)^21, 20);
- int
- This command can be used to calculate the indefinite or
definite integral of an expression f with respect to a variable x.
To compute the indefinite integral
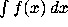 use
use
int(f, x);
To compute the definite integral 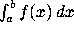 use
use
int(f, x=a..b);
To numerically evaluate the definite integral 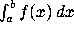 , use
, use
evalf(Int(f, x=a..b));
For example, the indefinite integral of 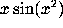 is
is
int(x*sin(x^2), x); while a definite integral is
int(x*sin(x^2), x=0..sqrt(Pi));
QUESTION 3: What is the exact value of  ? What is approximate numerical value?
? What is approximate numerical value?
- limit
- This command computes the limit of f as x approaches
a.
limit(f,x=a);
- simplify
- This command simplifies the expression entered. It has
several options associated to it.
simplify(expr);
For example, simplify( (x+3)^3 - (x-3)^3 );
- solve, fsolve
- These commands can be used to solve an equation or
set of equations for a variable or set of variables. The fsolve command
solves the equations numerically for real solutions, whereas
solve may give complex numbers as solutions.
The syntax is
solve({equations},{variables});
fsolve({equations},{variables});
For example, solve( {x-y=3, 3*x-2*y=-1}, {x,y} );
will solve for values of x and y that satisfy the two equations.
The fsolve command sometimes doesn't find all of the roots of an
equation. If you know how many roots you expect to find, you can use
the option fsolve( -4*x^3 + 4*x + 1, x, maxsols=3 );
- subs
- This is a powerful command that enables you to substitute
in a value (or a new expression) for some portion of an expression.
The syntax is
subs(subexpression=newexpression, expression );
For example, if you want to evaluate the expression 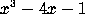 when
x=3:
when
x=3: subs(x=3, x^3-4*x-1 ); Or if you want to substitute
a more complicated expression (perhaps x is parametrized by
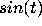 :
: subs(x=sin(t), x^3-4*x-1 );
Linear Algebra
The following commands are found in the package linalg. In order to use
these commands, you should load the package linalg using the command
with(linalg);.
- vector
- To enter a vector of length m with entries in a list use
vector(m,[list]);
If you omit the parameter m, a vector is created of length equal to the
number of elements on the list. If you eliminate the list parameter, Maple
creates a vector of length m with no predefined elements.
For example, vector([1,2,3]) sets up the vector with components
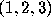 . Often we can shorten this notation (see the next example)
since many operations on vectors accept lists.
. Often we can shorten this notation (see the next example)
since many operations on vectors accept lists.
- crossprod
- This command computes the cross product of two
vectors of length 3.
To compute the cross product of the vectors u and v use
crossprod(u, v);
For example, crossprod([1,2,3], [4,5,6]);
- dotprod
- This command computes the dot product of two vectors of
length n.
To compute the dot product of the vectors u and v use
dotprod(u, v);
For example, dotprod([1,2,3], [4,5,6]);
- grad
- This command computes the gradient of a scalar function
of several variables.
For example, to compute the gradient of the function
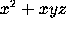 use
use
grad(x^2+x*y*z, [x,y,z]);
- diverge
- This command computes the divergence of a vector field.
For example, to compute the divergence of the vector field
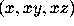 , use
, use
diverge([x,x*y,x*z], [x,y,z]);
- curl
- This command computes the curl of a vector field.
for example, to compute the curl of the vector field
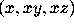 , use
, use
curl([x,x*y,x*z], [x,y,z]);



Next: Plotting with Maple
Up: Maple for Vector
Previous: Basic Maple Syntax
Bob Hesse
Wed Oct 23 21:17:40 CDT 1996
 , xn use
, xn use
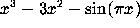 is
computed by
is
computed by
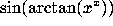 ?
?
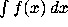 use
use
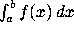 use
use
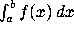 , use
, use
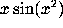 is
is
 ? What is approximate numerical value?
? What is approximate numerical value?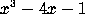 when
x=3:
when
x=3: 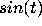 :
: 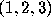 . Often we can shorten this notation (see the next example)
since many operations on vectors accept lists.
. Often we can shorten this notation (see the next example)
since many operations on vectors accept lists.
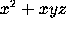 use
use
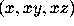 , use
, use
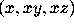 , use
, use