You will have two weeks to complete this lab, professionally write up
the answers, and submit it for a grade.
The purpose of the lab is
- to understand gradient vector fields and
their relationship with higher-dimensional surfaces and level sets of
those surfaces;
- to explore the geometry and discover
the relationships between a surface, gradients to that surface, and
the ``gradient flow'' on that surface.
- to see how multivariate functions naturally give rise to
gradient differential equations.
Background:
One of the greatest achievements of Newton (indeed, of all
mathematicians!) was formulating the
mathematics of gravitational attraction. Newton published his laws of
gravitation in his famous book, Principia Mathematica, in 1687. We
will not subject you to Newton's original formulation of gravitational
laws as it appeared in latin, but instead summarize in English: two
objects separated by a distance r feel a gravitational force due to
each other. The magnitude of this force is proportional to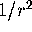 
.
It turns out that the gravitational force field is a so-called
``gradient field.'' This means that the force at any point is actually
the gradient of some function, called the ``gravitational potential
function.'' An important way to visualize gravitational force fields
is to visualize the graph of the gravitational potential function.
In order to simplify the mathematics, we assume that we are only
concerned about the gravitational field in a plane. This is actually a
close approximation to reality, since most of the objects in the solar
system (with the exception of pluto and some comets) essentially lie
in a plane (called the ``ecliptic plane''). Also, since we are
concentrating on the geometry, we will scale the physical equations so
that we do not need to worry about physical quantities such as the
mass of the earth or the distance from the earth to a satellite or to
the moon.
We begin by considering the gravitational force felt by a satellite in
space. We place the earth at the center of our coordinate system. We
then define the gravitational potential function to be
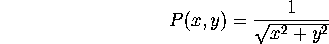
and the force felt by
an object located at position (x,y) to be
To get started, launch Maple and type in the following three commands:
with(linalg): with(plots):
P := -1/sqrt(x^2 + y^2);
F := grad( -P, [x,y] );
Note that we have defined the force to be the ``minus gradient'' of
the potential function.
Notice also that the
the potential is a function from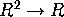 
, whereas the force is vector-valued.
QUESTION 1: Compute the magnitude of the force.
Is it the case that the magnitude is proportional to 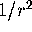where
r is the distance from the object to the origin?
Activity: (Activities do not need to be submitted as
part of the lab report.) Use Maple to visualize the graph of the
potential function on the domain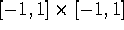 
.
Hint: you may want to add the option
view= -4..0 to your plot3d command. (See
?plot3d[options] to read about what this option does.)
Now think about placing a ball on the graph of the potential function.
When the ball is far away from the origin, the potential surface is
only slightly tilted, so the ball feels only a small force
towards the origin. If
the ball is near the origin, however, the potential surface is very steep,
so the ball feels a very strong pull towards the origin.
Mathematically, we say that the force felt by an object is the
negative of the gradient of the potential function.
Let's see how this all works:
QUESTION 2:
Answer the following questions:
- Compute the force felt by a particle at location
(x,y)=(1,1). This is a vector; call it v=F(1,1).
- Think of v as being based at the point (1,1). What
direction does v point and what is its magnitude?
QUESTION 3:
Use the Maple command
gradplot( -P, x=-1..1, y=-1..1, grid=[5,5]);
to visualize the ``vector field'' F at a few locations.
How does the plot of these vectors relate to the graph of the
potential function that we saw earlier? Mention both the magnitude
and the direction of the vectors.
QUESTION 4:
The gradient vector at a point has an interesting mathematical
relationship to the level sets of the function that passes through the
same point.
Use the contourplot command to look at the contours of the potential
function, or interactively change the previous 3D plot to show
contours. (Hint: again, you may want to tag on the option
view=-4..0 inside your Maple command. Also check into the option
contours=40.)
How do the contours relate to the gradient vectors that we
computed earlier?
In the second part of this lab we will use Matlab to study the ``lines
of force'' that are solutions to a certain differential equation
related to the gradient vector field. For now:
QUESTION 5:
Explain (using your knowledge of the physical
situation) what would happen if an object was placed somewhere in the
gravitational force field we've been looking at. Assume the object
starts at rest, and describe how its position, velocity, and
acceleration changes as time increases. We don't need any
sophisticated formulas here, just describe in words and/or pictures what you
think will happen. Conjecture what would happen if the object does
not start at rest.
For the next question, we will change the scenario under
consideration and ask you to investigate the new situation.
Assume that instead of one gravitational mass at the origin, we have
two gravitational masses. The one mass (say, the earth) is located at
(x,y)=(-1,0) and is very massive; the other mass (say, the moon) is
located at (x,y)=(0,1) and is less massive. In actuality, the
moon has about 1/100 the mass of the earth; we will use a ``massive
moon'' in order to make the geometry more apparent. In particular, we
will model the geometry of this new situation by
the gravitational potential function and the new force
field (in Maple notation) by
P := -1/sqrt((x+1)^2 + y^2) - 1/10/sqrt((x-1)^2 + y^2);
F := grad( -P, [x,y] );
QUESTION 6: Your task is to use Maple to investigate the gravitational
potential function for this new scenario. (Hint: You may want to
choose your plotting range differently than for the previous example.)
Explain what the potential surface looks like and what the
gravitational force field looks like. Also, conjecture as to how an
object (initially at rest) will move in this force field. Does the
object's ultimate fate depend on where the object begins? Is there any
location where the object could be placed where it would not move at
all?
At this point in the lab, we begin using Matlab to investigate the
same problem. Caution: the trajectories you will see are NOT
trajectories of an object in orbit around a gravitational body! It is
possible to compute such trajectories (we will do this briefly at the
end of the lab), but the computation requires looking at a
differential equation in which the positions and velocities
evolve in time. This requires looking at a four-dimensional
differential equation. For now, we will look at the gradient
differential equation
If we write this differential equation in vector form, the right-hand
side of the equation is just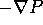 
. The solution to this
differential equation gives us the ``lines of gravitational force'' for this
gravitational system. If instead of gravitational bodies we were
considering charged bodies, then the solutions would be ``lines of
electromagnetic force.'' We could also consider magnetically charged
bodies to get lines of ``magnetic force.''
QUESTION 7: Start Matlab and invoke PPLANE. Using the potential
function for a single gravitational mass (from Question 1), define the
differential equation above by typing in each component of the
expression for 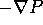into the PPLANE panel. Generate
trajectories of the gradient flow starting from
various initial conditions. What is the relationship between the
trajectories of the gradient flow and the level sets of the potential
function? Describe the ultimate fate of all trajectories as time
increases. That is, where do they end up?
QUESTION 8: Using the potential function for two gravitational
masses (from Question 6), define the corresponding gradient
differential equation using the PPLANE panel. Generate trajectories of
the gradient flow starting from
various initial conditions.
- questions here!
About this document ...
Return to Labs Homepage
Return to Calculus 3353/3354 Homepage
URL: http://www.geom.umn.edu/~math335x/Labs/Lab04/Lab04.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to:
hesse@math.umn.edu
Last modified: Oct 31 1996
The University of Minnesota is an equal opportunity educator and employer.