Next: The Geometry Center's 6-foot icosahedron
Up: Table of Contents
Prev: Assembling the structure

Exercise: How big is Your Icosahedron?

Ask the students to measure or calculate how large their icosahedron is. This may generate a discussion about what we mean by "how large." The icosahedron has both a "long diameter" (from one vertex to the opposite vertex) and a "short diameter" (from one face to the opposite face). Can the students relate these quantities to inscribed and circumscribed spheres?

The "long diameter" (widest part) of an icosahedron may be calculated from the edge length of the icosahedron. It turns out that the diameter is

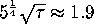
times larger than the side length, where

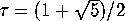
is a constant called the "golden mean." Can the students derive this quantity (very hard, especially if the students aren't familiar with trigonometry!) or experimentally determine the quantity by measuring the diameters and edge lengths of several icosahedra?

Can the students calculate the surface area of the icosahedra? What about obtaining an estimate of volume? Estimating the radius of inscribed and circumscribed spheres may help the students provide an upper and lower bound on the volume.

Next: The Geometry Center's 6-foot icosahedron
Up: Table of Contents
Prev: Assembling the structure
[HOME] The Geometry Center Home Page

Author: Frederick J. Wicklin <fjw@geom.umn.edu>
Comments to: webmaster@geom.umn.edu
Created: Summer 1994 --- Last modified: Jul 21 1996
Copyright © 1994-1996 by The Geometry Center All rights reserved.