Course projects
Next: The angle defect
Up: Geometry and the Imagination
Previous: Geometry on the
We expect everyone to do a project for the course. On the last day of
the course, Friday, June 28th, we will hold a Geometry Fair, where
projects will be exhibited. Parents and any other interested people
are invited.
Here are some ideas, to get you started thinking about possible projects.
Be creative-don't feel limited by these ideas.
- Write a computer program that allows the user to
select one of the
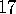 planar symmetry groups, start doodling,
and see the pattern replicate, as in Escher's drawings.
planar symmetry groups, start doodling,
and see the pattern replicate, as in Escher's drawings.
- Write a similar program for drawing tilings of the
hyperbolic plane, using one or two of the possible hyperbolic symmetry groups.
- Make sets of tiles which exhibit various kinds of
symmetry and which tile the plane in various symmetrical patterns.
- Write a computer program that replicates three-dimensional
objects according to a three-dimensional pattern, as in the tetrahedron,
octahedron, and icosahedron.
- Construct kaleidoscopes for tetrahedral, octahedral and
icosahedral symmetry.
- Construct a four-mirror kaleidoscope, giving a three-dimensional
pattern of repeating symmetry.
-
The Archimidean solids are solids whose faces are regular
polygons (but not necessarily all the same) such that every vertex is symmetric
with every other vertex. Make models of the the Archimedean solids
- Write a computer program for visualizing four-dimensional
space.
- Make stick models of the regular four-dimensional solids.
- Make models of three-dimensional cross-sections of
regular four-dimensional solids.
- Design and implement three-dimensional tetris.
- Make models of the regular star polyhedra
(Kepler-Poinsot polyhedron).
-
Knit a Klein bottle, or a projective plane.
-
Make some hyperbolic cloth.
-
Sew topological surfaces and maps.
- Infinite Euclidean polyhedra.
- Hyperbolic polyhedra.
- Make a (possibly computational) orrery.
- Design and make a sundial.
- Astrolabe (Like a primitive sextant).
- Calendars: perpetual, lunar, eclipse.
- Cubic surface with 27 lines.
- Spherical Trigonometry or Geometry: Explore spherical trigonometry or
geometry. What is the analog
on the sphere of a circle in the plane? Does every spherical triangle
have a unique inscribed and circumscribed circle? Answer these and other similar questions.
- Hyperbolic Trigonometry or Geometry: Explore hyperbolic trigonometry or
geometry. What is the analog
in the hyperbolic plane of a circle in the Euclidean plane? Does every hyperbolic triangle
have a unique inscribed and circumscribed circle? Answer these and other similar questions.
- Make a convincing model showing how a torus can be filled
with circular circles in four different ways.
- Turning the sphere inside out.
- Stereographic lamp.
- Flexible polyhedra.
- Models of ruled surfaces.
- Models of the projective plane.
- Puzzles and models illustrating extrinsic topology.
- Folding ellipsoids, hyperboloids, and other figures.
- Optical models: elliptical mirrors, etc.
- Mechanical devices for angle trisection, etc.
- Panoramic polyhedron (similar to an astronomical globe)
made from faces which are photographs.
Next: The angle defect
Up: Geometry and the Imagination
Previous: Geometry on the
Peter Doyle
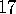 planar symmetry groups, start doodling,
and see the pattern replicate, as in Escher's drawings.
planar symmetry groups, start doodling,
and see the pattern replicate, as in Escher's drawings.
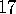 planar symmetry groups, start doodling,
and see the pattern replicate, as in Escher's drawings.
planar symmetry groups, start doodling,
and see the pattern replicate, as in Escher's drawings.