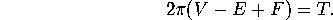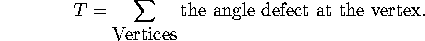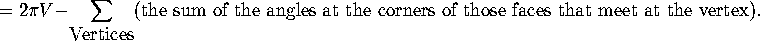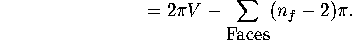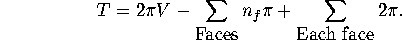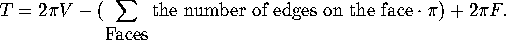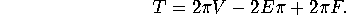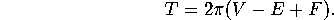Descartes's Formula.
Next: Exercises in imagining
Up: Geometry and the Imagination
Previous: The angle defect
The angle defect at a vertex of a polygon was defined to be the amount
by which the sum of the angles at the corners of the faces at that vertex
falls short of 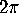 and the total angle defect of the polyhedron was defined to be what one got when one added up the
angle defects at all the vertices of the polyhedron.
We call the total defect
and the total angle defect of the polyhedron was defined to be what one got when one added up the
angle defects at all the vertices of the polyhedron.
We call the total defect 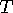 .
Descartes discovered that there is a connection between the total defect,
.
Descartes discovered that there is a connection between the total defect, 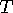 , and the Euler Number
, and the Euler Number 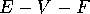 . Namely,
. Namely,
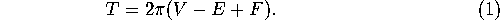
Here are two proofs. They both use the fact that the sum of the
angles of a polygon with  sides is
sides is 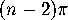 .
.
Think of 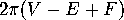 as putting
as putting 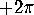 at each vertex,
at each vertex,
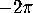 on each edge, and
on each edge, and 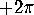 on each face.
on each face.
We will try to cancel out the terms as much as possible, by grouping
within polygons.
For each edge, there is 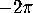 to allocate. An edge has a polygon on
each side: put
to allocate. An edge has a polygon on
each side: put 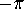 on one side, and
on one side, and 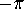 on the other.
on the other.
For each vertex, there is 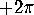 to allocate: we will do it according to
the angles of polygons at that vertex. If the angle of a polygon at
the vertex is
to allocate: we will do it according to
the angles of polygons at that vertex. If the angle of a polygon at
the vertex is  , allocate
, allocate  of the
of the 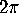 to that polygon.
This leaves something at the vertex: the angle defect.
to that polygon.
This leaves something at the vertex: the angle defect.
In each polygon, we now have a total of the sum of its angles minus
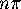 (where
(where  is the number of sides) plus
is the number of sides) plus 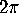 . Since
the sum of the angles of any polygon is
. Since
the sum of the angles of any polygon is 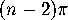 , this is 0.
Therefore,
, this is 0.
Therefore,
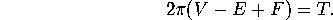
We begin to compute:
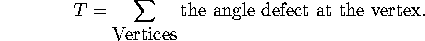

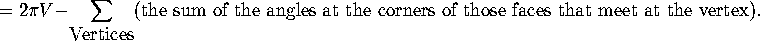

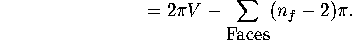
Here

denotes the number of edges on the face

.
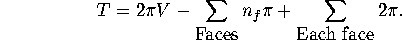
Thus
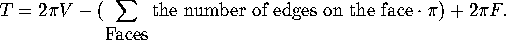
If we sum the number of edges on each face over all of the faces, we will have counted each edge twice. Thus
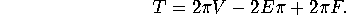
Whence,
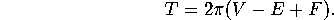
Listen to both proofs given in class.
- Discuss both proofs with the aim of understanding them.
- Draw a sketch of the first proof in the blank space above.
- Discuss the differences between the two proofs. Can you describe the
ways in which they are different? Which of you feel
the first is easier to understand? Which of you feel the second is easier
to understand? Which is more pleasing? Which is more conceptual?
Next: Exercises in imagining
Up: Geometry and the Imagination
Previous: The angle defect
Peter Doyle
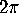 and the total angle defect of the polyhedron was defined to be what one got when one added up the
angle defects at all the vertices of the polyhedron.
We call the total defect
and the total angle defect of the polyhedron was defined to be what one got when one added up the
angle defects at all the vertices of the polyhedron.
We call the total defect 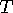 .
Descartes discovered that there is a connection between the total defect,
.
Descartes discovered that there is a connection between the total defect, 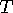 , and the Euler Number
, and the Euler Number 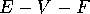 . Namely,
. Namely,
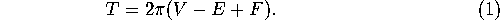
 sides is
sides is 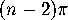 .
.
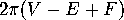 as putting
as putting 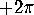 at each vertex,
at each vertex,
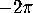 on each edge, and
on each edge, and 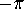 on one side, and
on one side, and  , allocate
, allocate 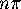 (where
(where