Next: 8.4 The Peano Curve and Fractal Curves
Up: 8 Special Plane Curves
Previous: 8.2 Roulettes (Spirograph Curves)
A number of interesting curves have polar equation r=f( ),
where f is a monotonic function (always increasing or decreasing).
This property leads to a spiral shape. The logarithmic spiral or
Bernoulli spiral (Figure 1, left) is
self-similar: by rotation the curve can be made to match any scaled
copy of itself. Its equation is r=k
),
where f is a monotonic function (always increasing or decreasing).
This property leads to a spiral shape. The logarithmic spiral or
Bernoulli spiral (Figure 1, left) is
self-similar: by rotation the curve can be made to match any scaled
copy of itself. Its equation is r=k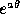 ; the angle between
the radius from the origin and the tangent to the curve is constant,
and equal to
; the angle between
the radius from the origin and the tangent to the curve is constant,
and equal to 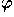 =arccot a. A curve parametrized by
arclength and such that the radius curvature is proportional to the parameter
at each point is a Bernoulli spiral.
=arccot a. A curve parametrized by
arclength and such that the radius curvature is proportional to the parameter
at each point is a Bernoulli spiral.
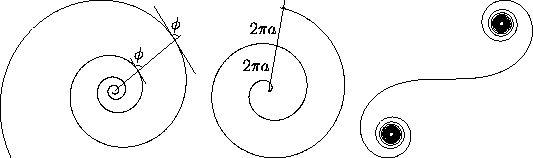
Figure 1: The Bernoulli or logarithmic spiral (left), the Archimedes
or linear spiral (middle), and the Cornu spiral (right).
In the Archimedean spiral or linear spiral
(Figure 1, middle), it is the spacing between
intersections along a ray from the origin that is constant. The
equation of this spiral is r=a ; by scaling one can take
a=1. It has an inner endpoint, in contrast with the logarithmic
spiral, which spirals down to the origin without reaching it. The
Cornu spiral or clothoid (Figure 1, right),
important in optics and engineering,
has the following parametric representation in Cartesian coordinates:
; by scaling one can take
a=1. It has an inner endpoint, in contrast with the logarithmic
spiral, which spirals down to the origin without reaching it. The
Cornu spiral or clothoid (Figure 1, right),
important in optics and engineering,
has the following parametric representation in Cartesian coordinates:

(C and S are the so-called Fresnel integrals; see
the
Standard Math Tables and Formulas.)
A curve parametrized by arclength and such
that the radius curvature is inversely proportional to the parameter at each
point is a Cornu spiral (compare the Bernoulli spiral).
Next: 8.4 The Peano Curve and Fractal Curves
Up: 8 Special Plane Curves
Previous: 8.2 Roulettes (Spirograph Curves)
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
 ),
where f is a monotonic function (always increasing or decreasing).
This property leads to a spiral shape. The logarithmic spiral or
Bernoulli spiral (Figure 1, left) is
self-similar: by rotation the curve can be made to match any scaled
copy of itself. Its equation is r=k
),
where f is a monotonic function (always increasing or decreasing).
This property leads to a spiral shape. The logarithmic spiral or
Bernoulli spiral (Figure 1, left) is
self-similar: by rotation the curve can be made to match any scaled
copy of itself. Its equation is r=k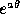 ; the angle between
the radius from the origin and the tangent to the curve is constant,
and equal to
; the angle between
the radius from the origin and the tangent to the curve is constant,
and equal to 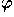 =arccot a. A curve parametrized by
arclength and such that the radius curvature is proportional to the parameter
at each point is a Bernoulli spiral.
=arccot a. A curve parametrized by
arclength and such that the radius curvature is proportional to the parameter
at each point is a Bernoulli spiral.


![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page