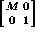is the 4×4
projective matrix obtained from the 3×3 matrix M by
adding a row and a column as stated.)
Next: 11 Other Transformations of Space
Up: 10 Space Symmetries or Isometries
Previous: 10.1 Formulas for Symmetries in Cartesian Coordinates
All isometries of space can be expressed in homogeneous coordinates in
terms of multiplication by a matrix. As in the case of plane
isometries (Section 2.2), this means that the successive
application of transformations reduces to matrix multiplication. (In
the formulas below, 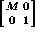is the 4×4
projective matrix obtained from the 3×3 matrix M by
adding a row and a column as stated.)
Translation by (x
,y,z):
Rotation through the origin:
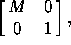where M is given in (10.1.1)
or (10.1.2)
, as
the case may be.
Reflection in a plane through the origin:
where M is given in (10.1.3)
.
From this one can deduce all other transformations, as in the case
of plane transformations 
.
![[HOME]](/pix/home.gif)
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.