 ,y
,y ,z
,z ), (x
), (x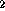 ,y
,y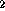 ,z
,z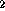 ) and
(x
) and
(x ,y
,y ,z
,z ) is given by
) is given by
Next: 13.1 Regular Polyhedra
Up: Part II: Three-Dimensional Geometry
Previous: 12.3 Lines
For any polyhedron topologically equivalent to a sphere---in particular, for any convex polyhedron---the Euler formula holds: v-e+f=2, where v is the number of vertices, e is the number of edges, and f is the number of faces.
Many common polyhedra are particular cases of cylinders (Section 13.2) or cones (Section 13.3). A cylinder with a polygonal base (directrix) is called a prism. A cone with a polygonal base is called a pyramid. A frustum of a cone with a polygonal base is called a trucated pyramid. Formulas (13.2.1) , (13.3.1) and (13.3.2) give the volume of a general prism, pyramid, and trucated pyramid.
A prism whose base is a parallelogram is a parallelepiped. The
volume of a parallelepiped with one vertex at the origin and
adjacent vertices at (x ,y
,y ,z
,z ), (x
), (x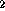 ,y
,y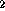 ,z
,z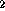 ) and
(x
) and
(x ,y
,y ,z
,z ) is given by
) is given by

The rectangular parallelepiped is a particular case: all its
faces are rectangles. If the side lengths are a, b,
c, the volume is abc, the total area is 2(
ab+ac+bc), and each diagonal has length
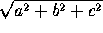 . When a=b=c we get the
cube: see Section 13.1.
. When a=b=c we get the
cube: see Section 13.1.
A pyramid whose base is a triangle is a tetrahedron. The
volume of a tetrahedon with one vertex at the origin and
the other vertices at (x ,y
,y ,z
,z ), (x
), (x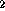 ,y
,y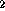 ,z
,z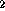 ) and
(x
) and
(x ,y
,y ,z
,z ) is given by
) is given by

In a tetrahedron with vertices P , P
, P , P
, P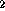 , P
, P , let
, let
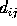 be the distance (edge length) from
be the distance (edge length) from 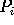 to
to 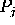 . Form the
determinants
. Form the
determinants

Then the volume of the tetrahedron is 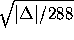 , and
the radius of the circumscribed sphere is
, and
the radius of the circumscribed sphere is 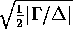 .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.