 ,y
,y ,z
,z ) parallel to the vector (a,b,c):
) parallel to the vector (a,b,c):
Next: 13 Polyhedra
Up: 12 DirectionsPlanes and Lines
Previous: 12.2 Planes
Two planes that are not parallel or coincident intersect in a straight line, so one can express a line by a pair of linear equations
ax+by+cz+d=0 and a'x+b'y+c'z+d'=0
such that bc'-cb', ca'-ac', and ab'-ba' are not all zero. The line thus defined is parallel to the vector
(bc'-cb', ca'-ac', ab'-ba').
The direction cosines of the line are those of this vector: see (12.1.1) . (The direction cosines of a line are only defined up to a simultaneous change in sign, since the opposite vector still gives the same line.)
The following particular cases are important:
Line through (x ,y
,y ,z
,z ) parallel to the vector (a,b,c):
) parallel to the vector (a,b,c):
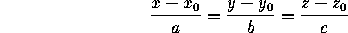
Line through (x ,y
,y ,z
,z ) and (x
) and (x ,y
,y ,z
,z ):
):
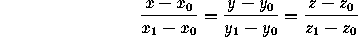
This line is parallel to the vector (x -x
-x , y
, y -y
-y ,
z
,
z -z
-z ).
).
The distance between two points in space is the length
of the line segment joining them. The distance between the points
(x ,y
,y ,z
,z ) and (x
) and (x ,y
,y ,z
,z ) is
is
) is
is
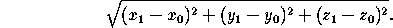
The point k% of the way from P =(x
=(x ,y
,y ,z
,z )
to P
)
to P =(x
=(x ,y
,y ,z
,z ) is
) is
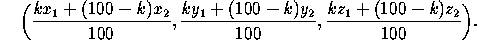
(The same formula works also in oblique coordinates.) This point
divides the segment P P
P in the ratio k:(100-k). As a
particular case, the midpoint of P
in the ratio k:(100-k). As a
particular case, the midpoint of P P
P is given by
is given by
(½(x +x
+x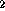 ),
½(y
),
½(y +y
+y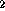 ),
½(z
),
½(z +z
+z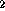 )).
)).
The Distance between the point (x ,y
,y ,z
,z ) and the line
through (x
) and the line
through (x ,y
,y ,z
,z ) in direction (a,b,c):
) in direction (a,b,c):
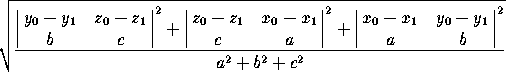
Distance between
the line through (x ,y
,y ,z
,z ) in direction (a
) in direction (a ,b
,b ,c
,c ) and
the line through (x
) and
the line through (x ,y
,y ,z
,z ) in direction (a
) in direction (a ,b
,b ,c
,c ):
):
Angle between lines with directions (x ,y
,y ,z
,z ) and
(x
) and
(x ,y
,y ,z
,z ):
):
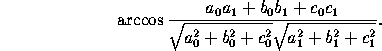
In particular, the two lines are parallel when a :b
:b :c
:c =
a
=
a :b
:b :c
:c , and perpendicular when a
, and perpendicular when a a
a +b
+b b
b +c
+c c
c =0.
=0.
Angle between lines with direction angles

 ,
,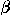
 ,
,
 and
and

 ,
,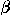
 ,
,
 :
:
arccos( cos 
 cos
cos 
 +
cos
+
cos 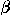
 cos
cos 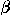
 +
cos
+
cos 
 cos
cos 
 )
)
Two lines specified by point and direction are coplanar if and only if the determinant in the numerator of (1) is zero. In this case they are concurrent (if the denominator is nonzero) or parallel (if the denominator is zero).
Three lines with directions (a ,b
,b ,c
,c ), (a
), (a ,b
,b ,c
,c ) and
(a
) and
(a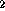 ,b
,b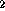 ,c
,c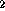 ) are parallel to a common plane if and only if
) are parallel to a common plane if and only if

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.