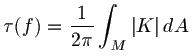
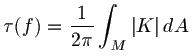
![[More]](pix/Link.gif) .
When equality holds, the mapping is called tight.
.
When equality holds, the mapping is called tight.
This definition turns out to have several important geometric consequences and equivalent definitions:
![[Right]](pix/Right.gif) Tightness and the convex hull.
Tightness and the convex hull.
![[Right]](pix/Right.gif) Tightness and polar height functions.
Tightness and polar height functions.
![[Right]](pix/Right.gif) Tightness and the two-piece property.
Tightness and the two-piece property.
![[Right]](pix/Right.gif) Tightness and homology: the modern definition.
Tightness and homology: the modern definition.
![[Right]](pix/Right.gif) Tightness for polyhedral surfaces.
Tightness for polyhedral surfaces.
![[Left]](pix/Left.gif) Kuiper's original question
Kuiper's original question
![[Up]](pix/Up.gif) Introduction
Introduction
7/21/94 dpvc@geom.umn.edu --
The Geometry Center