Non-Euclidean Geometry



Next: Minimal Surfaces
Up: Manifolds
Previous: Viewing with 4D
Mathematicians in the nineteenth century showed that it was possible
to create consistent geometries in which Euclid's Parallel Postulate
was no longer true- Absence of parallels leads to spherical, or
elliptic, geometry; abundance of parallels leads to hyperbolic
geometry. By mid-century the English mathematician Arthur Cayley had
constructed analytic models of these three geometries that had a
common descent from projective geometry, which one may think of as the
formalization of the renaissance theory of perspective. Cayley's
construction is in fact ideal for programming
interactive navigations of nonEuclidean geometries [10].
Many manifolds are naturally suited for hyperbolic or spherical,
rather than Euclidean, geometry. Although the formulas for computing
distance and angles in these geometries differ from Euclidean
geometry, they can be built into mathematical visualization systems by
hand. Translations, rotations, and dot-products for shaders and
illumination must also be handled differently in the non-Euclidean
geometries. In Figure
8, we see a partial tessellation of regular right-angled
dodecahedra in the three built-in Geomview models of hyperbolic
3-space. In the virtual model shown in Figure 8a, the
user can fly around to see the tessellation from the insider's point of
view. The other two models are from the outsider's point of view, and
we can see the position of the insider's camera marked by the blue X.
In the projective (Beltrami-Klein) model of hyperbolic space,
shown in Figure 8b,
geodesics (the paths of light rays) are Euclidean straight lines,
while angles are non-Euclidean in character.
In the conformal (Poincaré) model, on the other
hand, angles are measured by Euclidean protractors, but light
rays travel along circular arcs as in Figure 8c.
Figure 9, from the animation Not Knot (Sidebar
B),
shows us what an insider in an interesting hyperbolic 3-manifold would experience.
This 3-manifold is obtained by gluing the faces
of a right-angled dodecahedron (an impossibility in Euclidean
space) in a way analogous to our imaginary barbershop.
The projective models of non-Euclidean geometry can
be represented by 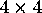 real matrix transformations
on homogeneous coordinates that are
serendipitously supported by
today's computer graphics transformation hardware and software
[10].
The conformal model, however, cannot be implemented using
real matrix transformations
on homogeneous coordinates that are
serendipitously supported by
today's computer graphics transformation hardware and software
[10].
The conformal model, however, cannot be implemented using
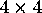 real matrices, so standard computer graphics hardware
does not suffice. Furthermore, the lines between edge endpoints
as well as the faces themselves are curved,
thus requiring subdivision of polygon edges and faces
into small line segments and polygons in order to draw
them as curves in computer graphics. Thus, the graphics
in the conformal model is
considerably slower than in the other two models.
real matrices, so standard computer graphics hardware
does not suffice. Furthermore, the lines between edge endpoints
as well as the faces themselves are curved,
thus requiring subdivision of polygon edges and faces
into small line segments and polygons in order to draw
them as curves in computer graphics. Thus, the graphics
in the conformal model is
considerably slower than in the other two models.
In all cases, however, the standard built-in illumination
computations are implicitly Euclidean; correct rendering of surface
shading requires custom software shaders that use alternative inner
products for computing distances and angles in non-Euclidean geometry.
Such shaders have been implemented and shown in [3]
to impose only moderate
performance penalties in comparison to the built-in Euclidean ones.
Such interactive tools for the exploration of non-Euclidean spaces
show clearly how computer graphics can allow humans to experience worlds
that otherwise would not be accessible. Direct
manipulation of non-Euclidean rotation and translation allows us to
develop an intuition for non-Euclidean behavior that we would be hard
put to gain in any other way. For research mathematicians, it
provides a microscope for investigating the diverse world of
three-dimensional manifolds.
Not all technical problems in geometrical visualization stem from
complicated manifolds, dimensions higher than three, or the challenge
of representing non-Euclidean geometry. Problems imposing strong
geometric constraints on the evolution of surfaces in ordinary 3D
space are also of great potential interest.
The remaining parts of this section deal with two
important domains of this type: minimal surfaces - surfaces that
minimize curvatures or energy functionals
- and regular homotopies - manifold deformations
whose curvatures remain finite at every point. The latter treatment
focuses on a particularly fascinating regular homotopy, the sphere
eversion.



Next: Minimal Surfaces
Up: Manifolds
Previous: Viewing with 4D
Tamara Munzner
Thu Sep 21 19:17:33 CDT 1995
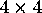 real matrix transformations
on homogeneous coordinates that are
serendipitously supported by
today's computer graphics transformation hardware and software
[10].
The conformal model, however, cannot be implemented using
real matrix transformations
on homogeneous coordinates that are
serendipitously supported by
today's computer graphics transformation hardware and software
[10].
The conformal model, however, cannot be implemented using
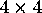 real matrices, so standard computer graphics hardware
does not suffice. Furthermore, the lines between edge endpoints
as well as the faces themselves are curved,
thus requiring subdivision of polygon edges and faces
into small line segments and polygons in order to draw
them as curves in computer graphics. Thus, the graphics
in the conformal model is
considerably slower than in the other two models.
real matrices, so standard computer graphics hardware
does not suffice. Furthermore, the lines between edge endpoints
as well as the faces themselves are curved,
thus requiring subdivision of polygon edges and faces
into small line segments and polygons in order to draw
them as curves in computer graphics. Thus, the graphics
in the conformal model is
considerably slower than in the other two models.