Surfaces in 4D



Next: Knotted Surfaces in
Up: Manifolds
Previous: What is a
During the seventies, Thomas Banchoff and his collaborators
pioneered a mathematical visualization
program at Brown university. They achieved interactive, real-time
geometrical visualizations of surfaces projected from 4D to 3D
with a custom-built matrix multiplier and
a fast-refresh vector graphics display for wire-frame modelling.
They also explored techniques such as enhancing depth perception
by rotating the resulting 3D object at
a constant angular velocity, and produced many animations
of classical objects such as projective planes and tori
projected from 4D to a 3D graphics depiction.
In Figure
1, we show an image of a classic Klein bottle
generated by this group that exhibits two separate visualization
methods: the use of a color code to indicate 4D depth and
a surface rendered with alternating transparent ribbons to reveal some
internal structure of the self-intersecting surface.
At the University of North Carolina/Chapel Hill, the Fourphront system
by David Banks is another interactive system for the study of surfaces
in 4D [1]. This system, which runs on the high-speed
massively parallel Pixel-Planes 5 graphics engine, provides user
control of transparency, depth cueing, intersection highlights, and
2-sided paint as well as supporting user control of rotation and
translation. An illustration of Fourphront's alternative approach to
the Klein bottle display is shown in Figure 3.
Another influential development was Apéry's presentation in 1984 of
a long sought parametric equation for Boy's surface, a classic
immersion of the projective plane in 3D whose purely topological
description dates to the turn of the century. Apéry also formulated
the ``Romboy homotopy''
a smooth deformation between his own parametrization of Boy's surface
and Steiner's Roman Surface, another projective plane
whose parametrization as a 4D surface had been known for a century.
George Francis and his collaborators Donna Cox and Ray
Idaszak exploited this work to create an animation, ``The Etruscan Venus,''
whose title refers to the suggestive shape of a
singular Klein bottle that appears in the deformation.
An additional deformation leads to a new, highly symmetrical
immersion of the Klein bottle dubbed ``Ida,'' which graced the cover of
the August 1989 issue of IEEE Computer. The animation editor
used to produce the Etruscan Venus and Ida has evolved
into the highly interactive real-time
illiView collection of mathematical animators, produced principally by
students taught by George Francis in the Renaissance Experimental
Laboratory at the National Center for Supercomputing Applications
(NCSA) at
the University of Illinois. Figure 4 shows an
example of a current illiView visualization.
In 1987, the Geometry Supercomputer Project was created at the University
of Minnesota, and subsequently evolved to become the Geometry Center,
a National Science and Technology Research Center, in 1991. The
Center has served as a focal point for a number of efforts
in mathematical visualization;
a widely used system distributed by the Geometry Center is
Geomview [9], a very general surface viewer
developed by Stuart Levy, Tamara Munzner, and
Mark Phillips.
Its built-in functionality can be extended by customized
user programs, called external modules. While Geomview
is fundamentally a 3D viewer, the
4DView external module by Daeron Meyer supplied with Geomview
accepts 4D data points, allows the user to
change the 4D viewpoint, and
includes tools for creating 4D slices. Another external module,
NDView by Olaf Holt and Stuart Levy, interacts with
objects of dimension 4 and higher using multiple projections
into families of 3D subspaces. A typical Geomview surface
display is shown in Figure 16.
A 4D viewer with a different philosophy is the MeshView program
designed by Hui Ma and Andrew Hanson of Indiana University. This
system supports the Geomview 4D surface mesh data format, but in addition
provides a high-speed mouse-driven 4D rotation interface and a
utility for locating particular points on a projected surface relative
to the abstract parametric mesh coordinates.
Figure 5 illustrates a MeshView
display of the 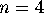 case of a
closed-form construction developed by Andrew Hanson for
representing the complex ``Fermat'' equations
case of a
closed-form construction developed by Andrew Hanson for
representing the complex ``Fermat'' equations 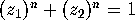 ; the surface is projected from 2 complex dimensions to 3 real
dimensions from any desired viewpoint. Large families of
complex surfaces can be displayed interactively in MeshView
using this technique.
; the surface is projected from 2 complex dimensions to 3 real
dimensions from any desired viewpoint. Large families of
complex surfaces can be displayed interactively in MeshView
using this technique.



Next: Knotted Surfaces in
Up: Manifolds
Previous: What is a
Tamara Munzner
Thu Sep 21 19:17:33 CDT 1995
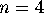 case of a
closed-form construction developed by Andrew Hanson for
representing the complex ``Fermat'' equations
case of a
closed-form construction developed by Andrew Hanson for
representing the complex ``Fermat'' equations 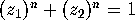 ; the surface is projected from 2 complex dimensions to 3 real
dimensions from any desired viewpoint. Large families of
complex surfaces can be displayed interactively in MeshView
using this technique.
; the surface is projected from 2 complex dimensions to 3 real
dimensions from any desired viewpoint. Large families of
complex surfaces can be displayed interactively in MeshView
using this technique.