Moments of Inertia

Angular vs. Linear Motion

For linear motion, Newton's second law relates the acceleration of a particle of mass m to the force F applied to it. In symbols,

F = m a .

From the equation (and common sense) it is clear that a larger force is required to accelerate a more massive particle. Intuitively, the mass of the particle resists acceleration. We say that the mass gives the particle linear inertia.

For angular (rotational) motion, the angular acceleration depends not only on the applied force, but also on where the force is applied in relation to the axis of rotation (or "pivot point"). For this reason, as we observed in the last section, it is the torque a force generates which is most naturally related to the angular acceleration of the particle.

Torque plays the same role in rotating systems that force plays in linear motion. However, the resistance to angular acceleration again depends on both the mass of the particle and its distance from the axis of rotation. Therefore we introduce a new quantity called the moment of inertia to measure resistance to angular acceleration. The moment of inertia of a rotating system is analogous to the mass of a linearly accelerating system.

Using Newton's second law, one can show that the relationship between the torque, T , and the angular acceleration, A , of a particle is given by

T = (m r ^²) A .

Thus, we define the moment of inertia to be the quantity mr ^² of the particle. The moment of inertia is typically denoted by I .

Formulas for Systems and Continuous Objects

For a rigid configuration of particles, the moment of inertia is simply the sum of all the individual moments. For a continuous distribution of mass, just as with the center of mass, we proceed by chopping the object into tiny elements of mass, and, for each element, add up the moment of inertia due to that mass. As before, these approximations to the moment of inertia converge to the true moment.

In general, computing the moment of inertia can be quite difficult, requiring the more sophisticated techniques of iterated integrals from multivariable calculus. However, when an object is sufficiently symmetrical, we can compute the moment of inertia with a standard one-variable integral.

Now consider a planar object as in Figure 4, and imagine rotating it about the x -axis. (Note it is rotating out of the xy -plane into the third dimension perpendicular to your computer screen.) This might represent, for example, a model of a rotating turbine blade as it rotates around its central spindle.

Figure 4: Slicing an irregular object into strips.

In this case, note that the entire strip indicated in the figure remains at a constant distance from the axis of rotation. Therefore, this strip has the same moment of inertia as a particle of the same mass lying at the same distance above the x -axis.

If we assume that the object has been cut out of some thin material of uniform density p , the mass of the strip is simply p w(y) dy . Consequently, it's moment of inertia is

p y ^² w(y) dy .

It follows that the moment of inertia for the whole object is given by the formula

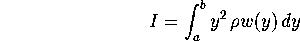
where a and b are the minimum and maximum values of the y variable.

Question 3

Find the moment of inertia for a rectangle of length l and width w when the axis of rotation is
1. the centerline of the rectangle, and
2. one of the edges.
In order to make a building wheelchair-accessible, an engineer is told to double the width of a revolving door. By how much will this increase the moment of inertia? What practical issues might the engineer need to worry about if the door width is doubled?

Question 4

Because computing moments of inertia directly can be quite laborious, people have worked out indirect ways of computing unknown moments of inertia from known moments. In particular, if we know the moment of inertia of an object around one axis of rotation, it turns out that we can find the moment of inertia for the same object about an axis that is parallel to the first axis without completely re-doing the problem! This useful result is known as the Parallel Axis Theorem.

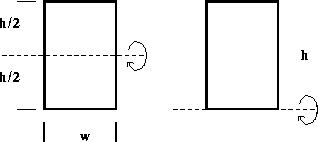
Answer the following questions by interacting with the Exploring Moments of Inertia page.

Experimentally determine the moment of inertia of a C-beam around various horizontal axes of rotation. Record your data in a table.
Where does the minimum moment of inertia occur? Conjecture a relationship between this point and other geometric properties of the object.
If you graph your data, it should look like a familiar function: a quadratic function! Try to fit your data with a quadratic function of the form M(y-C) ^² + I_min .
Try to give physical interpretations to the constants M and C for your model function. In particular, we would expect from physical considerations that the moment of inertia depends on the object's mass and on its shape. How do these quantities relate to the model function you found?

Next: Modeling Deflections in Beams
Return to: Centers of Mass and Centroids
Up: Outline

The Geometry Center Calculus Development Team