 Click on the picture to see a movie.
Click on the picture to see a movie.

When studying symmetry groups of surfaces, we also learn about symmetry groups of real life objects; chairs, for instance. "Wait," you say, "chairs aren't surfaces!" True. Chairs are solid objects, but we don't yet have the tools to deal with symmetries of solid objects -- we're going to translate the 3D chair into a 2D pattern that we can easily deal with.
Imagine surrounding the chair by a sphere, so that the center of the sphere is at the center of symmetry of the chair. Then every plane of mirror symmetry of the chair cuts the sphere in a line of mirror symmetry of the sphere, and every rotatinal symmetry of the chair is a rotational symmetry of the surface of the sphere. In this way, the symmetries of the 3D solid chair corresponds to a symmetry of the surface of the sphere.
If you're disturbed that the surface of the sphere is more symmetric
than the chair inside it, put a bomb at the center of symmetry of the
chair. When the bomb explodes, the splattered bits of the chair will
make a pattern on the surface of the sphere. The symmetries of the
chair will exactly correspond to symmetries of this pattern.
 Click on the picture to see a movie.
Click on the picture to see a movie.
Although it is harder to cut and fold spherical regions, we can still define orbifolds for the symmetries of three dimensional objects like chairs and tables. The mirror string in the symmetry group of our chair is a great circle on the surface of the celestial sphere. The chair has no rotational symmetry (the orbifold has no cone points), and there are no corners on the orbifold, so the symbol for this symmetry group is just *.
We can identify pairs of points that are mirror reflections of each
other on the surface of this sphere by punching one side of the sphere
inwards. (Imagine punching the left side of a ball until the ball
deflates and the left and right sides coincide.) This leaves us with
the surface of a hemispherical bowl with the line of mirror symmetry
as its rim. This is the orbifold for the symmetry group of the chair.
 Take a piece of celestial chalk and a plain rectangular table
surrounded by the celestial sphere. Draw the lines of mirror symmetry
of the table on the sphere with the chalk. (If you don't have any
celestial chalk, just draw them with ordinary chalk on the surface of
the table.) The two lines of mirror symmetry of the table become
great circles on the sphere that meet at right angles. The orbifold
of the table looks like the peel from a quarter of an orange. Since
the two corners of the orbifold are distinct (the top of the table
looks different from the bottom of the table), the symbol is *22; this
is another discopic group.
Take a piece of celestial chalk and a plain rectangular table
surrounded by the celestial sphere. Draw the lines of mirror symmetry
of the table on the sphere with the chalk. (If you don't have any
celestial chalk, just draw them with ordinary chalk on the surface of
the table.) The two lines of mirror symmetry of the table become
great circles on the sphere that meet at right angles. The orbifold
of the table looks like the peel from a quarter of an orange. Since
the two corners of the orbifold are distinct (the top of the table
looks different from the bottom of the table), the symbol is *22; this
is another discopic group.
Click on the picture to see a movie.
Exercise: Cut an orange in quarters along the planes of symmetry of the table and eat one quarter of the orange. The emptied peel is a model of the orbifold.
Knowing the symmetries of an object can be a powerful tool; if we are
building a skyscraper with *22 symmetry, we only have to design one
quarter of it!
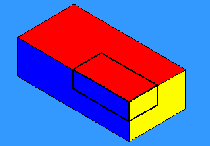

The symmetry group of a brick is discopic, like that of the table,
except that the top of a brick is the same as the bottom. Its group is
*222, and a model of its orbifold is the peel from one of the eight
three cornered pieces that the orange is cut into by the three
coordinate planes. In general, groups denoted *22n are called
"prismatic". Groups denoted 2*n are "polydigyros."
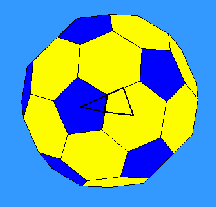
A soccer ball (truncated icosahedron) has lots of mirror line great circles. These meet in fives at centers of pentagonal faces, in threes at centers of hexagonal faces, and in twos at midpoints of edges. The orbifold is one of the 120 triangles into which the sphere is cut by these lines. This is exactly the triangle outlined by the KaleidoTile program, shown above. Since its boundary has one 5-way, one 3-way, and one 2-way mirror point, its type is *532 and its group (the achiral icosahedral group) is pentascopic.
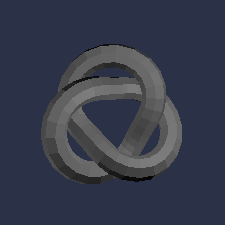 Not all examples are as simple as the ones above. Consider the
trefoil knot shown in the picture. It has order three rotational
symmetry and no lines of reflection. When we encase it in a sphere,
we see two order three gyration points at the poles of the sphere. To
construct the orbifold, we can first cut a slit from one pole the
other, and curl the sphere up so that it overlaps itself three times
-- once for each of the three lobes of the knot. It will then look
something like an American football. This "tritropic" orbifold has
two cone points and is denoted 33; groups with orbifold notation nn
are called "polytropic".
Not all examples are as simple as the ones above. Consider the
trefoil knot shown in the picture. It has order three rotational
symmetry and no lines of reflection. When we encase it in a sphere,
we see two order three gyration points at the poles of the sphere. To
construct the orbifold, we can first cut a slit from one pole the
other, and curl the sphere up so that it overlaps itself three times
-- once for each of the three lobes of the knot. It will then look
something like an American football. This "tritropic" orbifold has
two cone points and is denoted 33; groups with orbifold notation nn
are called "polytropic".
If the top and bottom of the trefoil knot are different, this is exactly the orbifold of the knot. However, if the top and bottom of the knot are alike, we will find some order two gyration points on the equator of the celestial sphere. To completely construct the orbifold of the knot we must add another order two cone-point to the equator of the football shaped orbifold. The orbifold notation for this symmetric knot would then be 332.
Notice that even when the trefoil has only one rotational symmetry, it
gets two digits in the orbifold notation. The characters in the
notation correspond to features of the orbifold rather than
to elements of the symmetry group. As Thurston discovered, this often
makes it easier to study such symmetry groups. Please always remember
and never forget that the symbols in the notation correspond to
features of the orbifold, but not necessarily to group elements
(though they usually come quite close).
Perhaps you've noticed that the numbers appearing in the orbifold notation for spherical symmetry groups are smaller and/or fewer than the numbers that appear when studying planar symmetry groups. That is, in fact, the case, as the next page of this lab will show.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Heidi Burgiel
Comments to:
webmaster@geom.umn.edu
Created: Dec 7 1995 ---
Last modified: Jul 31 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.