Next: Another Look at the Linkage
Up: Peaucellier's Linkage Table of Contents
Prev: Create the Linkage

Peaucellier's Linkage

Part 2. Inversion

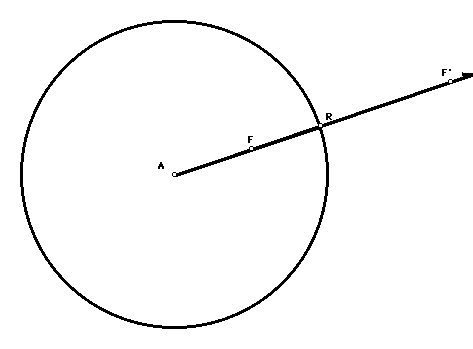
Given a circle in the plane, you now study a transformation of the plane associated with this circle called inversion through the circle. In other words, given a point F in the plane, there is another point F' called the inverse of F. The picture below shows a circle of inversion, a point F and its inverse F'. Although inversion may seem an artificial construct, it has many powerful applications in mathematics and physics.

Here is how you determine the inverse of F through a circle with center A and radius r. (Refer to the picture.) Draw a ray starting at A passing through F. The inverse F' of F is the point on the ray such that:

(AF)(AF')=r^2

Another way to write this: If R is the point of intersection between the circle and the ray, then

(AF')= [(AR)/(AF)] (AR)


A. Construct the inverse

Now use Sketchpad to construct the inverse of a given point through a given circle. When you are done, make the process into a script. Doing so will save you a lot of time.

  1. Start with a circle of inversion and a point F to invert.

  2. Construct the ray from A through F. Find the point R of intersection between the circle and the ray.

  3. Use a dilation centered at A. Dilate point R by marked ratio. (Remember that to mark a ratio, you need to select two segments and choose the Mark Ratio option on the Transform menu.) By looking at the formula above, determine this ratio. What is it? This dilation gives you the inverse point F'.

  4. Hide the ray and the point R. You only want to see how F' changes as you move F.

B. Investigate inversion using your sketch

Investigate the following set of questions. Think about them in terms of the definition of inversion as well as by investigation in Sketchpad.
  1. Where is the inverse of a point inside the circle?

  2. Where is the inverse of a point outside the circle?

  3. Are there points that are their own inverses?

  4. Where is the inverse of the center of the circle?

C. The inverses of circles and lines

As a point goes around a circle, its inverse traces out a shape. The shape traced out is called the inverse of the circle. Investigate the following questions about the inverses of circles and lines. Again, try to answer the questions first by thinking about them and then by using Sketchpad. Use the answers to fill out the chart below.
  1. What is the inverse of a circle? Trace this using Sketchpad.
  2. What happens to the inverse when your circle intersects point A, the center of the circle of inversion?
  3. What is the inverse of a line? Trace this using Sketchpad.
  4. What happens to the inverse when your line goes through point A?

Shape ______________________________ Inverse of the shape

Circle through A

Circle not through A

Line through A

Line not through A


D. Constructing inverses of circles and lines

You know how to construct a line using two points on the line. You know how to construct a circle using three points on the circle. Use this and your table to do the following:
  1. Find the inverse of a circle c passing through point A.
    Hint: Start by constructing the inverses of two points on the circle.

    Test your construction: as a point goes around the circle, does its inverse always lie on the shape you constructed?

  2. Construct the inverse of a line not through A. Again, test your construction.

Next: Another Look at the Linkage
Up: Peaucellier's Linkage Table of Contents
Prev: Create the Linkage
[HOME] The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@geom.umn.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996