Peaucellier's Linkage

Part 3. Another look at the Linkage

A. The linkage and inversion

1. Comparing the chart you made in the section on inversion, to the shapes traced out by P and Q, is it possible that P and Q are related by inversion?

2. If so, where would P, Q, and the center of the circle of inversion all lie? What other property would P, Q, and the center of the circle satisfy?

3. Find a point on the linkage that satisfies these properties as P moves around the circle. (Hint: You may want to use the Calculator on the Measure menu to measure a product. What has to be true of this constant as P moves?)

4. Once you have found the point satisfying the definition, points P and Q must be inverses through some circle of inversion. Therefore from your chart, you know the shape that Q traces. However, go on and actually find the circle of inversion and construct the path traced by Q as follows.

B. Constructing the circle of inversion

Using your product, you know the radius of the center of inversion. What is it? Although you know it, since it is a measured quantity, you need to find it in another way in order to construct the circle of inversion: Since the radius is a constant independent of the position of the linkage, it depends only on the three fixed length segments you made off to the side. What is the relationship? This is a pen and paper exercise using the Pythagorean theorem. Here are some pictures of specific cases to help you form a conjecture for a general equation for the radius of the circle of inversion. In the first picture, P and Q lie on top of each other. In the second, R and S lie on top of each other. In each case, can you state the radius of the circle of inversion in terms of the segments j, k, and m?

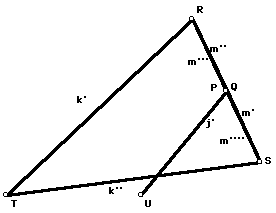
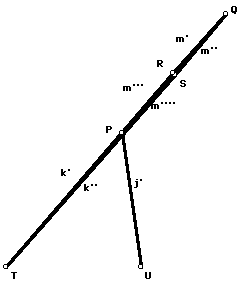
Finally, use the circle of inversion you constructed and your method for constructing the inverse of a circle to construct the shape traced by Q. Check that Q does lie on this shape as you move P.

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@geom.umn.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996