Computing the Envelope of a Family of Curves

Figure 5: The nephroid as an envelope of light rays.

In general, suppose we have a family of curves C varying with t, (like our different lines reflected from the light ray at y=t) and C_t is defined by an equation F(t,x,y)=0. A curve E is said to be part of the envelope of the family if it shares a tangent line with each curve C_t. We would like to be able to compute an equation for curves in the envelope for this family, but this may be difficult. It is also possible that no such envelope curves exist.

However, when F(t,x,y) is a polynomial function of all 3 variables t,x,y, there is a way to use elimination of variables to compute the equation of a curve containing an envelope to the family C_t. This is explained in Projection, profiles, envelopes.

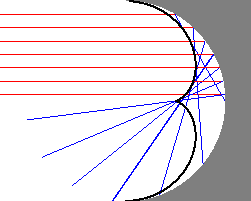
The idea goes like this. The equation F(t,x,y)=0 defines a surface in 3-dimensional (x,y,t)-space. In the case of our family of reflected line this surface is built geometrically as a "ruled surface" by stacking up each reflected light ray in sequence. Click here to see an MPEG movie (478 Kbytes) of this process. Of course, the complete surface is not merely the union of the reflected rays that come in from the left (as in Figure 5), but also includes the union of rays that reflect off the left-hand side of the coffee cup.

As explained in Projection, profiles, envelopes, the points of the envelope are the projections onto the xy-plane of those points on this surface F(t,x,y)=0 for which the tangent plane is parallel to the t-axis. This leads us to look for the equation of the envelope curves by eliminating the variable t from the equations

F(t,x,y) = 0
d/dt F(t,x,y) = 0

In order to do this for our family of reflected lines C_t, we must first express their equations in the form F(t,x,y) = 0, i.e. we must get rid of the square root occurring in the equation that we already found, and then bring all the terms to one side.

Question 6

• Show that you can manipulate the equation we found for the line reflected from y=t so that there is only a single product involving a square root sitting alone on one side of the equation.
• Now square both sides of the equation to get rid of the square root, and bring all the terms to one side to obtain something of the form F(t,x,y)=0 for some polynomial F(t,x,y) in the variables t,x,y. Compare your answer with the one we got:

  F(t,x,y) = ((y-t)(2-t²) + t(4-t²))² - t²x²(4-t²)

> F:=((y-t)*(2-t^2)+t*(4-t^2))^2-t^2*x^2*(4-t^2);

                        2            2  2    2  2       2
    F := ((y - t) (2 - t ) + t (4 - t ))  - t  x  (4 - t )

> GB:=gbasis({F,diff(F,t)},[t,x,y],plex):

> factor(GB[9]);

     2  2            2       2       4       2  2       4      6       4  2
    x  y  (- 4 + 12 x  - 15 y  - 12 x  - 24 x  y  - 12 y  + 4 x  + 12 x  y

               4  2      6
         + 12 y  x  + 4 y )

Question 7