

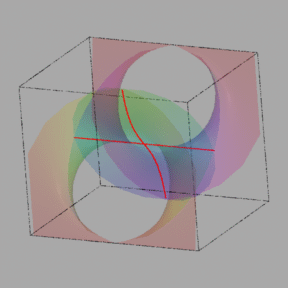
On the other hand, points on the curve/surface where the gradient is the zero vector do not have a well-defined tangent line/plane. These points are highlighted in the pictures below

f(x,y)=0
d/dx f(x,y)=0
d/dy f(x,y)=0
for an algebraic curve f(x,y)=0, and by the equations
F(t,x,y)=0
d/dx F(t,x,y)=0
d/dy F(t,x,y)=0
d/dt F(t,x,y)=0
for an algebraic surface F(t,x,y)=0. If one has a method for solving polynomial equations, then one can find the solutions to the above equations and compute the singular set of your curve/surface. For example, the Maple computations shown below give the singularities of the nephroid and the graph surface F(t,x,y)=0.
4 2 2 2 2 2 4 2 4 6
nephroid := 12 x y - 4 - 15 y + 12 x - 24 y x + 12 y x - 12 y + 4 y
4 6
- 12 x + 4 x
2 2 2 2 2 2
F := ((y - t) (2 - t ) + t (4 - t )) - t x (4 - t )
> solve({nephroid=0,diff(nephroid,x)=0,diff(nephroid,y)=0},{x,y});
2
{y = 0, x = 1}, {y = 0, x = -1}, {x = 0, y = RootOf(1 + 2 _Z )}
> solve({F=0,diff(F,x)=0,diff(F,y)=0,diff(F,t)=0},{t,x,y});
t
{x = x, y = 0, t = 0}, {t = t, x = 0, y = 2 --------},
2
- 2 + t
2 2
{x = 0, y = - 1/2 RootOf(2 + _Z ), t = RootOf(2 + _Z )}