A Simple Algorithm (Simple)
Overview
This algorithm traces the level set of a function of two
variables. This algorithm is not intended to be used when an
accurate approximation to a level curve is required. Rather,
this algorithm is a simple example of how to write an algorithm
in Pisces.
How the Simple Algorithm Works
The idea is, well, simple. The user specifies a bounding box and
two integers. The two integers determine the number of sub-boxes into
which the bounding box is subdivided. We will call the sub-boxes "cells."
The algorithm subdivides the bounding box into equal sized cells, then
evaluates the function at the corner of each cell.
For each cell, if all of the function evaluations have the same sign
(all positive or all negative), then we assume that there is no
solution to f=0 within the cell.
If at least two corners of a cell have different signs, then evaluate
the function along each edge and solve for points along the edge where
f=0. In this implementation, we only use a linear
approximation to the solution. The collection of points where
f=0 are then connected to each other (in the order they were
generated) with line segments.
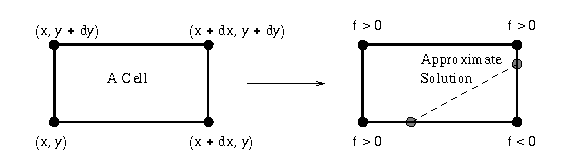
Schematic diagram of the simple algorithm.

The panel that controls the "simple algorithm."
Controlling the algorithm from Pisces
- HorDivisions
- This parameter determines the number of intervals into which the
horizontal side of the bounding box is divided.
EXAMPLE: If the bounding box is [0,1]x[-1,1]
and HorDivisions equals 4,
then we will subdivide the interval [0,1] into
four segments: [0,0.25], [0.25,0.5], [0.5,0.75], and [0.75,1].
The endpoints of these segments will be used as gridpoints
for evaluating the model.
- VerDivisions
- This parameter determines the number of intervals into which the
vertical side of the bounding box is divided.
Known Bugs
None, but the algorithm is extremely wasteful in the allocation of
memory and in the evaluation of the model. This was done
intentionally in order to make the algorithm as easy to understand as
possible. Please send bug reports to
software@geom.umn.edu.
Algorithm Implemented by
Frederick J. Wicklin
Next: Geisow's Algorithm
Previous: User Interface
![[Pisces]](../../../pix/pi.gif) The Pisces Home Page
The Pisces Home Page
Comments to: pisces@geom.umn.edu
Last modified: Tue Nov 28 10:06:50 1995
Copyright © 1995 by
The Geometry Center,
all rights reserved.
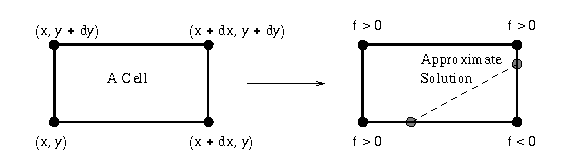

![[Pisces]](../../../pix/pi.gif) The Pisces Home Page
The Pisces Home Page