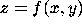Other Plot Routines

There are other types of plot routines that are useful for analyzing functions of two variables:

contourplot

To plot the level sets or contours of a function on a domain in the plane:

        contourplot(f(x,y),x=a..b,y=c..d);

For example,contourplot(-x^4+2*x^2-y^2,x=-1.6..1.6,y=-1.6..1.6); It is sometimes useful to tack an option like contours=40 onto the end of the contourplot command.

Note that smoother curves can be obtained by including a specification for the grid parameter of the form

        contourplot(f(x,y),x=a..b,y=c..d,grid=[k,k]);

where k is an integer. The default value of k is 25.

Notice that a contour plot is a three dimensional plot of the level curves of the function viewed from above. You can see this by rotating the plot as you did with 3D graphics.

densityplot

To plot a density plot of a function on a domain in the plane, use:

        densityplot(f(x,y),x=a..b,y=c..d);

In contrast with the contour plot, the density plot in Maple is a 2D object and cannot be rotated in space. For example, densityplot(-x^4+ 2*x^2-y^2,x=-1.6..1.6,y=-1.6..1.6);

display

This is a very powerful command because it allows you to combine two plots into one. It works with both plot and plot3d images. For example,

	Plot1 := plot(cos(x),x=-Pi..Pi, color=red): #Note the suppressed output
	Plot2 := plot(1 - x,x=-Pi..Pi, color=green): 
        display({Plot1, Plot2});

gradplot

To plot the gradient vector field of a function over a domain, use

        gradplot(f(x,y), x=a..b,y=c..d);

For example, the gradient vector field corresponding to the function 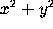is a vector field in which all vectors point radially outward from the origin: gradplot(x^2+y^2, x=-1..1,y=-1..1);

fieldplot

To plot a vector field over a domain, use

        fieldplot([f1(x,y),f2(x,y)], x=a..b,y=c..d);

For example, the vector field corresponding to the differential equation for a simple harmonic oscillator is plotted by fieldplot([y,-x], x=-1..1,y=-1..1);