Next: 3.3 Projective Transformations
Up: 3 Other Transformations of the Plane
Previous: 3.1 Similarities

3.2 Affine Transformations

A transformation that preserves lines and parallelism (maps parallel lines to parallel lines) is an affine transformation. There are two important particular cases of such transformations:

A nonproportional scaling transformation centered at the origin has the form

where 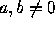are the scaling factors (real numbers). The corresponding matrix in homogeneous coordinates is

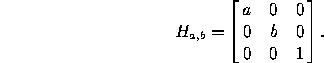
A shear preserving horizontal lines has the form

where r is the shearing factor (see Figure 1). The corresponding matrix in homogeneous coordinates is

  
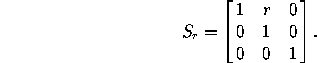
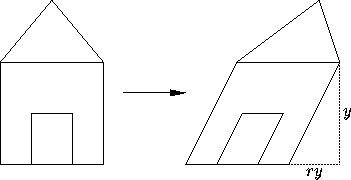
Figure 1: A shear with factor r=½.

Every affine transformation is obtained by composing a scaling transformation with an isometry, or a shear with a homothety and an isometry.

The Geometry Center Home Page

Silvio Levy
Wed Oct 4 16:41:25 PDT 1995

This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.