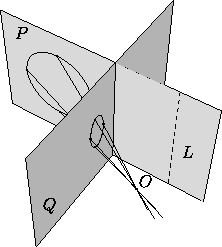
Figure 1: A perspective transformation with center O, mapping the plane P to the plane Q. The transformation is not defined on the line L, where P intersects the plane parallel to Q and going throught O.
Next: 4 Lines
Up: 3 Other Transformations of the Plane
Previous: 3.2 Affine Transformations
A transformation that maps lines to lines (but does not necessarily preserve parallelism) is a projective transformation. Any plane projective transformation can be expressed by an invertible 3×3 matrix in homogeneous coordinates; conversely, any invertible 3×3 matrix defines a projective transformation of the plane. Projective transformations (if not affine) are not defined on all of the plane, but only on the complement of a line (the missing line is ``mapped to infinity'').
A common example of a projective transformation is given by a perspective transformation (Figure 1). Strictly speaking this gives a transformation from one plane to another, but if we identify the two planes by (for example) fixing a cartesian system in each, we get a projective transformation from the plane to itself.

Figure 1:
A perspective transformation with center O, mapping the plane P to
the plane Q. The transformation is not defined on the line L,
where P intersects the plane parallel to Q and going throught O.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.