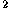 +b
+b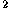 =1 and c
=1 and c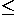 0 in the equation ax+by+c=0, the equation
is said to be in normal form. In this case c is the
distance of the line to the origin, and
0 in the equation ax+by+c=0, the equation
is said to be in normal form. In this case c is the
distance of the line to the origin, and
Next: 4.1 Distances
Up: Part I: Two-Dimensional Geometry
Previous: 3.3 Projective Transformations
The (cartesian) equation of a straight line is linear in the coordinates x and y, that is, of the form ax+by+c=0.
The slope of this line is -a/b, the intersection with the x-axis (or x-intercept) is x=-c/a, and the intersection with the y-axis (or y-intercept) is y=-c/b. If a=0 the line is parallel to the x-axis, and if b=0 the line is parallel to the y-axis.
(In an oblique coordinate system everything in the preceding paragraph remains true, except for the value of the slope.)
When a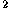 +b
+b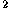 =1 and c
=1 and c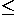 0 in the equation ax+by+c=0, the equation
is said to be in normal form. In this case c is the
distance of the line to the origin, and
0 in the equation ax+by+c=0, the equation
is said to be in normal form. In this case c is the
distance of the line to the origin, and
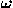 = arcsin a = arccos b
= arcsin a = arccos b
is the angle that the perpendicular dropped to the line from the origin makes with the positive x-axis (Figure 1).
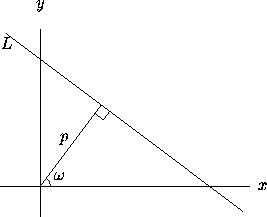
Figure 1: The normal form of L is
x cos 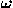 + y sin
+ y sin 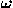 =p.
=p.
To reduce an arbitrary equation ax+by+c=0 to normal form, divide by
±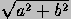 , where the sign of the radical is chosen opposite
the sign of c when c
, where the sign of the radical is chosen opposite
the sign of c when c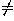 0 and the same as the sign of b when
c=0.
0 and the same as the sign of b when
c=0.
Line of slope m intersecting the x-axis at x=x :
:
y=m(x-x )
)
Line of slope m intersecting the y-axis at y=y :
:
y=mx+y
Line intersecting the x-axis at x=x and the
y-axis at y=y
and the
y-axis at y=y :
:
x/x +y/y
+y/y =1
=1
(This formula remains true in oblique coordinates.)
Line of slope m going though (x ,y
,y ):
):
y-y =m(x-x
=m(x-x )
)
Line going through points (x ,y
,y ) and (x
) and (x ,y
,y ):
):
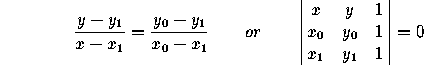
(These formulas remain true in oblique coordinates.)
Slope of
line going through points (x ,y
,y ) and (x
) and (x ,y
,y ):
):
(y -y
-y )/(x
)/(x -x
-x )
)
Line going through points with polar coordinates
(r ,
,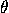
 ) and (r
) and (r ,
,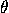
 ):
):
r(r sin(
sin(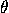 -
-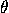
 )-r
)-r sin(
sin(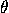 -
-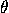
 ))=
r
))=
r r
r sin(
sin(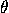
 -
-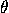
 ).
).
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.