Next: 1.5 Oblique Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1.3 Polar Coordinates in the Plane
A triple of real numbers (x:y:t), with t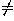 0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:t) and (x':y':t') represent the same
point if and only if there is some real number
0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:t) and (x':y':t') represent the same
point if and only if there is some real number  such that
x'=
such that
x'= x, y'=
x, y'= y, t'=
y, t'= t.
If P has cartesian coordinates (x
t.
If P has cartesian coordinates (x ,y
,y ), one set of homogeneous
coordinates for P is (x
), one set of homogeneous
coordinates for P is (x ,y
,y ,1).
,1).
When we think of the same triple of numbers as the cartesian
coordinates of a point in three-dimensional space
(Section 9.1), we write it (x,y,t) instead of
(x:y:t). The connection between the point in space with cartesian
coordinates (x,y,t) and the point in the plane with homogeneous
coordinates (x:y:t) becomes apparent when we consider the plane
t=1 in space, with cartesian coordinates given by the first two
coordinates x, y of space (Figure 1). The point
(x,y,t) in space can be connected to the origin by a line L that
intersects the plane t=1 in the point with cartesian coordinates
(x/t, y/t), or homogeneous coordinates (x:y:t).
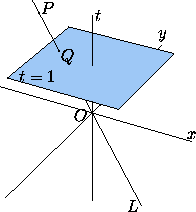
Figure 1: The point P with spatial coordinates (x,y,t) projects to
the point Q with spatial coordinates (x/t, y/t, 1). The plane
cartesian coordinates of Q are (x/t, y/t), and (x:y:t) is one
set of homogeneous coordinates for Q. Any point on the line L
(except for the origin O) would also project to P'.
Projective coordinates are useful for several reasons, one the most
important being that they allow one to unify all symmetries of the
plane (as well as other transformations) under a single umbrella. All
these transformations can be regarded as linear maps in the space of
triples (x:y:t), and so can be expressed in terms of matrix
multiplications. (See Section 2.2).
If we consider triples (x:y:t) such that at least one of x, y, t is
nonzero, we can name not only the points in the plane but also
points ``at infinity''. Thus (x:y:t) represents the point at
infinity in the direction of the line with slope y/x.
Next: 1.5 Oblique Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1.3 Polar Coordinates in the Plane
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
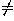 0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:t) and (x':y':t') represent the same
point if and only if there is some real number
0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:t) and (x':y':t') represent the same
point if and only if there is some real number  such that
x'=
such that
x'= x, y'=
x, y'= y, t'=
y, t'= t.
If P has cartesian coordinates (x
t.
If P has cartesian coordinates (x ,y
,y ), one set of homogeneous
coordinates for P is (x
), one set of homogeneous
coordinates for P is (x ,y
,y ,1).
,1).

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page