Next: 2 Plane Symmetries or Isometries
Up: 1 Coordinate Systems in the Plane
Previous: 1.4 Homogeneous Coordinates in the Plane
The following generalization of cartesian coordinates is sometimes
useful. Consider two axes (graduated lines), intersecting at the
origin but not necessarily perperdicularly. Let the angle
between them be 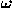 . In this system of oblique coordinates,
a point P is given by two real numbers indicating the positions of
the projections from the point to each axis, in the direction of the
other axis. See Figure 1. The first axis (x-axis)
is generally drawn horizontally. The case
. In this system of oblique coordinates,
a point P is given by two real numbers indicating the positions of
the projections from the point to each axis, in the direction of the
other axis. See Figure 1. The first axis (x-axis)
is generally drawn horizontally. The case 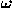 =90° yields
a cartesian coordinate system.
=90° yields
a cartesian coordinate system.
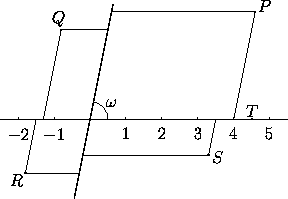
Figure 1: In oblique coordinates, P=(4,3),
Q=(-1.3,2.5), R=(-1.5,-1.5), S=(3.5,-1), and
T=(4.5,0). Compare Figure 1.2.1
.
Let the two oblique coordinate systems (x,y) and
(x',y'), with angles 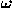 and
and 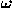 ',
share the same origin, and suppose the
x'-axis makes an angle
',
share the same origin, and suppose the
x'-axis makes an angle  with the x-axis. The coordinates
(x,y) and (x',y') of a point in the two systems are related by
with the x-axis. The coordinates
(x,y) and (x',y') of a point in the two systems are related by
x = (x' sin(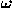 -
- ) + y'
sin(
) + y'
sin(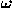 -
-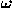 '-
'- ))/ sin
))/ sin 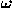 ,
,
y = (x' sin  + y' sin(
+ y' sin(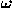 '+
'+ ))/ sin
))/ sin 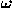 .
.
This formula also covers passing from a cartesian system to an oblique
system and vice versa, by taking 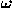 =90° or
=90° or 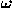 '=90°.
'=90°.
The relation between two oblique coordinate systems that differ by a
translation is the same as for cartesian systems: see
(1.1.4)
.
Next: 2 Plane Symmetries or Isometries
Up: 1 Coordinate Systems in the Plane
Previous: 1.4 Homogeneous Coordinates in the Plane
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
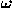 . In this system of oblique coordinates,
a point P is given by two real numbers indicating the positions of
the projections from the point to each axis, in the direction of the
other axis. See Figure 1. The first axis (x-axis)
is generally drawn horizontally. The case
. In this system of oblique coordinates,
a point P is given by two real numbers indicating the positions of
the projections from the point to each axis, in the direction of the
other axis. See Figure 1. The first axis (x-axis)
is generally drawn horizontally. The case 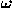 =90° yields
a cartesian coordinate system.
=90° yields
a cartesian coordinate system.

 with the x-axis. The coordinates
(x,y) and (x',y') of a point in the two systems are related by
with the x-axis. The coordinates
(x,y) and (x',y') of a point in the two systems are related by
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page