Next: 16 Quadrics
Up: Part II: Three-Dimensional Geometry
Previous: 14 Spheres

15 Surfaces of Revolution. The Torus

A surface of revolution is formed by the rotation of a planar curve C about an axis in the plane of the curve and not cutting the curve. The Pappus--Guldinus theorem says that:

• The area of the surface of revolution on a curve C is equal to the product of the length of C and the length of the path traced by the centroid of C (which is 2 the distance from this centroid to the axis of revolution).
• The volume bounded by the surface of revolution on a simple closed curve C is equal to the product of the area bounded by C and the length of the path traced by the centroid of the area bounded by C.

When C is a circle, the surface obtained is a circular torus or torus of revolution (Figure 1). Let r be the radius of the revolving circle and let R be the distance from its center to the axis of rotation. The area of the torus is 4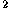Rr, and its volume is 2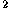Rr.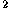

  
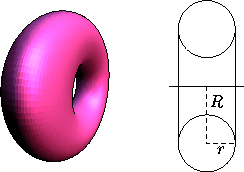
Figure 1: A torus of revolution.

The Geometry Center Home Page

Silvio Levy
Wed Oct 4 16:41:25 PDT 1995

This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.