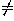Up: Part II: Three-Dimensional Geometry
Previous: 15 Surfaces of Revolution. The Torus


16 Quadrics

 

A surface defined by an algebraic equation of degree two is called a quadric. Spheres, circular cylinders, and circular cones are quadrics. By means of a rigid motion, any quadric can be transformed into a quadric having one of the following equations (where a,b,c0):

(1) Real ellipsoid x/a+y/b+z/c=1
(2) Imaginary ellipsoid x/a+y/b+z/c=-1
(3) Hyperboloid of one sheet x/a+y/b-z/c=1
(4) Hyperboloid of two sheets x/a+y/b-z/c=-1
(5) Real quadric cone x/a+y/b-z/c=0
(6) Imaginary quadric cone x/a+y/b+z/c=0
(7) Elliptic paraboloid x/a+y/b+2z=0
(8) Hyperbolic paraboloid x/a-y/b+2z=0
(9) Real elliptic cylinder x/a+y/b=1
(10) Imaginary elliptic cylinder x/a+y/b=-1
(11) Hyperbolic cylinder x/a-y/b=1
(12) Real intersecting planes x/a-y/b=0
(13) Imaginary intersecting planes x/a+y/b=0
(14) Parabolic cylinder x+2y=0
(15) Real parallel planes x=1
(16) Imaginary parallel planes x=-1
(17) Coincident planes x=0

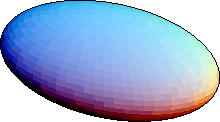
The five nondegenerate real quadrics

  
Figure 1: The ellipsoid (1).

 
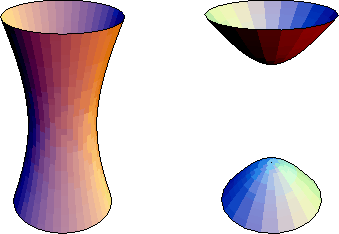
Figure 2: Left: hyperboloid of one sheet (3). Right: hyperboloid of two sheets (4).

  
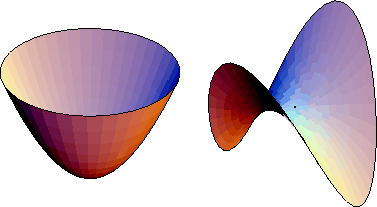
Figure 3: Left: elliptic paraboloid (7). Right: hyperbolic paraboloid (8).

Surfaces with equations (9) --(17) are cylinders over the planes curves of the same equation (Section 13.2). Equations (2), (6), (10), (16), have no real solutions, so they do not describe surfaces in real three-dimensional space. A surface with equation (5) can be regarded as a cone (Section 13.3) over a conic C (any ellipse, parabola or hyperbola can be taken as the directrix; there is a two-parameter family of essentially distinct cones over it, determined by the position of the vertex with respect to C). The real nondegenerate quadrics (1), (3), (4), (7), and (8) are shown in Figures 1--3.

The surfaces with equations (1) --(6) are central quadrics; in the form given, the center is at the origin. The quantities a, b, c are the semiaxes.

The volume of the ellipsoid with semiaxes a, b, c is 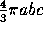. When two of the semiaxes are the same, we can also write the area of the ellipsoid in closed form. Suppose b=c, so the ellipsoid x/a+(y+z)/b=1 is the surface of revolution obtained by rotating the ellipse x/a+y/b=1 around the x-axis. Its area is

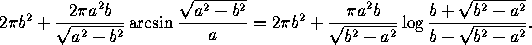
The two quantities are equal, but only one avoids complex numbers, depending on whether a>b or a<b. When a>b, we have a prolate spheroid, that is, an ellipse rotated around its major axis; when a<b we have an oblate spheroid, which is an ellipse rotated around its minor axis.

Given a general quadratic equation in three variables,

ax+by+cz+2fyz+2gzx+2hxy+2px+2qy+2rz+d=0,

one can find out the type of conic it determines by consulting the following table:

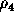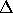k signs K signs Type of quadric
34<0real ellipsoid
34>0sameimaginary ellipsoid
34>0oppositehyperboloid of one sheet
34<0oppositehyperboloid of two sheets
33oppositereal quadric cone
33sameimaginary quadric cone
24<0sameelliptic paraboloid
24>0oppositehyperbolic paraboloid
23sameoppositereal elliptic cylinder
23samesameimaginary elliptic cylinder
23oppositehyperbolic cylinder
22oppositereal intersecting planes
22sameimaginary intersecting planes
13parabolic cylinder
12oppositereal parallel planes
12sameimaginary parallel planes
11coincident planes

The columns have the following meaning. Let

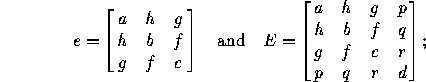
let 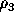and 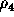be the ranks of e and E, and let 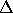be the determinant of E. The column ``k signs'' refers to the nonzero eigenvalues of e, that is, the roots of

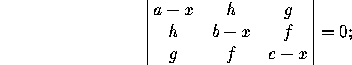
if all nonzero eigenvalues have the same sign, choose ``same'', otherwise ``opposite''. Similarly, ``K signs'' refers to the sign of the nonzero eigenvalues of E.

Up: Part II: Three-Dimensional Geometry
Previous: 15 Surfaces of Revolution. The Torus


[HOME] The Geometry Center Home Page

Silvio Levy
Wed Oct 4 16:41:25 PDT 1995

This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.