![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
It is very hard, if not impossible, to give a complete error analysis
for any algorithm that computes a global object like an unstable
manifold. Here we show that the distance between a first finite
piece 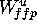 of
of
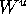 and its approximating
triangulation
and its approximating
triangulation 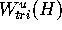 goes to zero with the initial distance from H and the mesh
size. We use that f is Lipschitz in a neighborhood of
goes to zero with the initial distance from H and the mesh
size. We use that f is Lipschitz in a neighborhood of
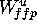 .
.
To fix terms, suppose that 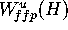 is the first finite piece of
is the first finite piece of
 of a normally hyperbolic
invariant circle H of saddle-type. (The argument goes through
for the unstable manifold of a hyperbolic fixed point as well.)
of a normally hyperbolic
invariant circle H of saddle-type. (The argument goes through
for the unstable manifold of a hyperbolic fixed point as well.)
Because  is bounded and f is at least
is bounded and f is at least 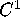 , we can always
find a finite constant
, we can always
find a finite constant  such that
such that 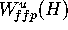 is
is
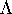 -Lipschitz in a neighborhood U. Furthermore, H is
normally hyperbolic, so that
-Lipschitz in a neighborhood U. Furthermore, H is
normally hyperbolic, so that 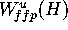 is even locally attracting if
it is contained in a small enough neighborhood of H. In other word,
for fixed
is even locally attracting if
it is contained in a small enough neighborhood of H. In other word,
for fixed 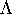 -Lipschitz
-Lipschitz 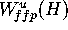 we can find a
we can find a 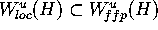 that is locally
that is locally 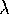 -attracting in a
neighborhood V, for a certain
-attracting in a
neighborhood V, for a certain 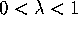 .
.
Let 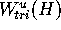 be the continuous approximation of
be the continuous approximation of 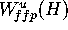 , given as
a triangulation in
, given as
a triangulation in Tri with mesh points in Mesh. For
simplicity we assume that 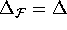 (see Section 3.4 for the definition of
(see Section 3.4 for the definition of 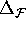 ). In other words, the mesh is uniform, and
). In other words, the mesh is uniform, and  describes
its quality. We like to think of
describes
its quality. We like to think of 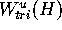 as a fixed object of which
we want to compute the distance
as a fixed object of which
we want to compute the distance  to
to 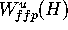 . If we change
. If we change
 , then
, then Tri and Mesh change accordingly, so that
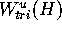 becomes a different object for which the distance
becomes a different object for which the distance  to
to 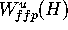 is different as well. We assume that
is different as well. We assume that 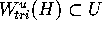 .
.
The idea is now to show that the error 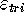 goes to zero as the
initial distance
goes to zero as the
initial distance 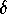 from H and the mesh width
from H and the mesh width  both go
to zero. For this we make use of the Lipschitz constants
both go
to zero. For this we make use of the Lipschitz constants 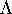 and
and
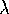 . Note that it is impossible to determine these constants in
practice if
. Note that it is impossible to determine these constants in
practice if 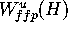 is a global object of reasonable size. In other
words, we cannot give an a priori error bound on the distance between
is a global object of reasonable size. In other
words, we cannot give an a priori error bound on the distance between
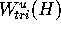 and
and 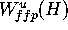 for given
for given 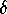 and
and  .
At the end of this section we discuss how the accuracy of
the approximation
.
At the end of this section we discuss how the accuracy of
the approximation 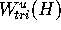 can be checked numerically.
can be checked numerically.
For technical reasons we need the error at the mesh points of
Mesh and the interpolation error.
If 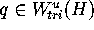 is not a mesh point, then the distance of q to
is not a mesh point, then the distance of q to
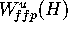 depends only on the distance of the mesh points to
depends only on the distance of the mesh points to
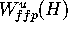 and the mesh width
and the mesh width  . Hence, the difference between
the global error
. Hence, the difference between
the global error 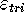 and the error
and the error 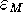 at the mesh points is
finite and depends on
at the mesh points is
finite and depends on  .
.
Clearly,  goes to zero as
goes to zero as 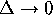 , since then
, since then
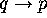 . If
. If 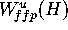 is
is 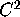 then
then 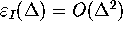 .
.
Proof of Theorem 3: Note that Definitions 2, 4 and 5 imply that
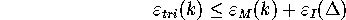
for all 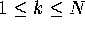 , where N+1 is the total number of circles
in
, where N+1 is the total number of circles
in Mesh. Hence, we need to show that 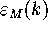 becomes
arbitrarily small as
becomes
arbitrarily small as 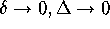 .
The idea is to estimate the error on
.
The idea is to estimate the error on 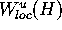 first and then
the error on the rest of
first and then
the error on the rest of 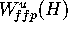 .
.
To this end, we now consider the first K+1 circles in Mesh,
where K depends on 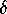 and
and  , and is such that for all
p =
, and is such that for all
p = Mesh[k][r] with 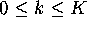 and
and 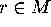
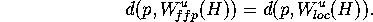
This means that the first K+1 circles in Mesh form an
approximation of 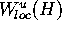 .
(Note that K = N if
.
(Note that K = N if 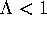 .) Since
the first two circles in
.) Since
the first two circles in Mesh are distance 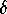 apart, we
can assume that K > 1 by taking
apart, we
can assume that K > 1 by taking 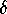 small enough. We also
assume that these K rings of
small enough. We also
assume that these K rings of  are contained in V, the
neighborhood on which f is a contraction.
are contained in V, the
neighborhood on which f is a contraction.
The initial error 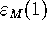 is the maximal distance
to
is the maximal distance
to 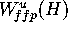 of the mesh points on the first two circles
of the mesh points on the first two circles
Mesh[0] and Mesh[1]. The mesh points of the circle
Mesh[0] are the points of M. With the algorithm in
[Osinga 1996,
Broer et al. 1996,
Broer et al. 1997] it is possible to ensure that the distance
of the points in M to H is at most 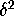 . The mesh points of
the circle
. The mesh points of
the circle Mesh[1] lie at distance  from
from
Mesh[0]. Consequently, we get for the initial error
at the mesh points 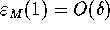 ,
because
,
because 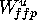 is at least
is at least
 . If
. If 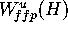 is
is 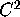 then
then 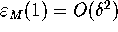 .
.
In the next step we express 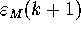 in terms of
in terms of 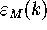 for
for
 . By definition
. By definition 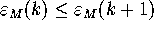 , but
it may happen that
the error in the
, but
it may happen that
the error in the 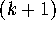 -st step does not increase, so that
-st step does not increase, so that
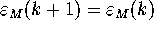 . Now suppose that
. Now suppose that 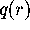 is
the point on
is
the point on  such that
such that Mesh[k+1][r] =
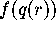 . By construction,
. By construction,  , and we have
, and we have
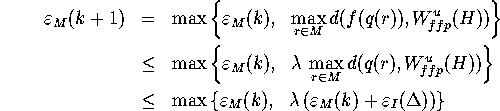
This shows that the error does not increase, if
 is small compared to
is small compared to 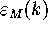 . Suppose the error
increases l times in the K steps that build the first K + 1
circles. This means that
. Suppose the error
increases l times in the K steps that build the first K + 1
circles. This means that
where the last inequality holds for all 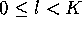 , because
, because 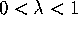 . Hence, the total error for the approximation of
. Hence, the total error for the approximation of
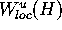 is bounded from above by:
is bounded from above by:
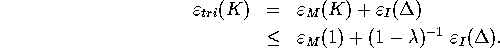
Clearly,
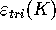 goes to zero as
goes to zero as 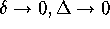 .
If
.
If 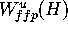 is
is 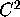 , then
, then 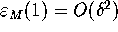 and
and
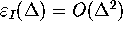 . Consequently,
. Consequently, 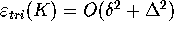 , which is the claimed result for
, which is the claimed result for 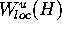 .
.
For the circles Mesh[k] with 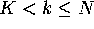 we need to
proceed more carefully. Again we concentrate on the error
we need to
proceed more carefully. Again we concentrate on the error
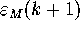 at the mesh points, where now
at the mesh points, where now 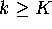 . As before, let
. As before, let
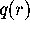 be the point on
be the point on 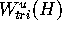 such that
such that Mesh[k+1][r]
= 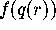 . If
. If 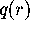 is contained in the part of
is contained in the part of 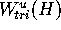 given by
the first K+1 circles, then we can immediately find a bound on the
error at
given by
the first K+1 circles, then we can immediately find a bound on the
error at 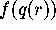 by using
Equation (2) and the
Lipschitz constant
by using
Equation (2) and the
Lipschitz constant 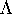 for f.
for f.
The idea is to count the number of iterations it takes to reach any
given point in
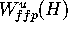 with a point in
with a point in 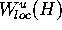 . This number
is finite, because
. This number
is finite, because 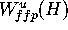 is bounded. Since we only have an
approximation of
is bounded. Since we only have an
approximation of 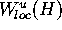 and
and 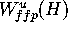 , we need to consider the
maximum number of itererates that a point from V spends in a
closed neighborhood
, we need to consider the
maximum number of itererates that a point from V spends in a
closed neighborhood 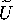 of
of 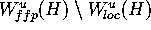 . Note that the neighborhood
. Note that the neighborhood
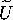 can be chosen such that
can be chosen such that 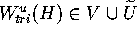 , because we have assumed that
, because we have assumed that 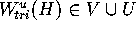 . Since
. Since 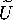 is compact, this maximal number of
iterates exists and we denote it by
is compact, this maximal number of
iterates exists and we denote it by 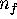 .
It is important to note that
.
It is important to note that 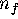 only depends on
only depends on 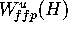 and
and 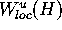 , so that it does not change if we decrease
, so that it does not change if we decrease 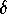 and/or
and/or
 .
.
Let  be
the point on
be
the point on  such that
such that Mesh[k+1][r] =
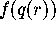 . Clearly,
. Clearly, 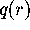 lies in ring i of
lies in ring i of  for some
for some
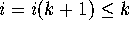 . Then
. Then
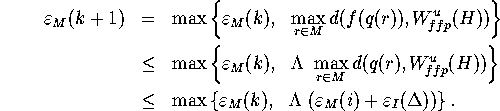
Hence, for any 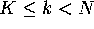 , either
, either 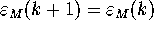 or we
can apply the inequality with
or we
can apply the inequality with  , However, we can do this at
most
, However, we can do this at
most 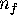 times before we reach
times before we reach 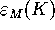 for which we already have
an upper bound in terms of
for which we already have
an upper bound in terms of  . Hence,
. Hence,
(Here we assume that 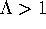 , because
otherwise K = N and
, because
otherwise K = N and 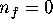 .)
Combining (2) and
(3) leads to
.)
Combining (2) and
(3) leads to
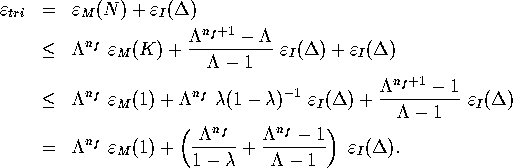
Because 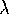 ,
,  and
and 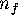 are constants,
are constants, 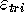 goes to zero with the same
order as
goes to zero with the same
order as 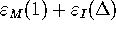 . If
. If 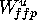 is
is 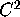 then
(1) follows.
then
(1) follows.
Remark 6
Note that the estimate does not depend on the accuracy
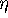 of the
bisection. In practice,
of the
bisection. In practice,
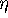 should be small to ensure
that f(q) lies approximately in the leaf
should be small to ensure
that f(q) lies approximately in the leaf
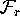 and at a distance
and at a distance
 from the last
point. However, the distance of f(q) to
from the last
point. However, the distance of f(q) to
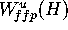 is
governed by the fact that q lies in a triangle of the
continuous object
is
governed by the fact that q lies in a triangle of the
continuous object 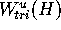 .
.
The error estimate in Theorem 3 is a theoretical
result. In practice, it is impossible to check if 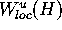 is locally
attracting, and to determine
is locally
attracting, and to determine 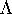 . However,
Theorem 3 suggests a strategy for numerically
checking if a computed piece
. However,
Theorem 3 suggests a strategy for numerically
checking if a computed piece 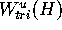 is close to
is close to 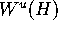 : repeat
the computation with a finer mesh and a smaller initial distance from
H to obtain a second approximation
: repeat
the computation with a finer mesh and a smaller initial distance from
H to obtain a second approximation  . If the
distance between
. If the
distance between 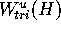 and
and 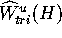 is small then it is
reasonable to assume that
is small then it is
reasonable to assume that 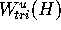 is indeed close to
is indeed close to 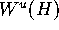 . We
have used this method to check the accuracy in the examples in
Section 5.
. We
have used this method to check the accuracy in the examples in
Section 5.
If there are periodic points on H, one can
compute their one-dimensional (strong) unstable manifolds, which lie in
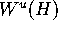 . Then
. Then 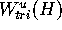 is close to
is close to 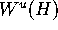 if these
one-dimensional objects lie in
if these
one-dimensional objects lie in  within the given accuracy;
compare Section 5.1. Furthermore, in
Section 5.3 we study a test example,
where the unstable manifold (of a fixed
point) is known analytically. This allows us to estimate the global
error numerically and monitor its growth.
within the given accuracy;
compare Section 5.1. Furthermore, in
Section 5.3 we study a test example,
where the unstable manifold (of a fixed
point) is known analytically. This allows us to estimate the global
error numerically and monitor its growth.
In summary, we have the confidence that our algorithm is capable of
computing a large piece of 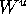 with sufficient accuracy, so
that statements on the global dynamics are possible. We refer to the
examples in the next section.
with sufficient accuracy, so
that statements on the global dynamics are possible. We refer to the
examples in the next section.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:52:54 1997