![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
The algorithm produces a mesh of points
on the unstable manifold 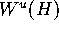 . This mesh is a
discrete object, and it is
represented by sequences of N+1 points,
where each sequence is a discretization of a piece
of the curve
. This mesh is a
discrete object, and it is
represented by sequences of N+1 points,
where each sequence is a discretization of a piece
of the curve
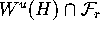 in
each of the leaves of
in
each of the leaves of 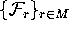 . We desribe the
algorithm in its simplest form, when the number
of leaves |M| remains fixed. Mesh
adaptation by adding leaves during the computation is
the topic of Section 3.4.
. We desribe the
algorithm in its simplest form, when the number
of leaves |M| remains fixed. Mesh
adaptation by adding leaves during the computation is
the topic of Section 3.4.
The mesh is computed in steps by adding a (discrete) circle to the
mesh of the previous step. This process is illustrated with an
animation.
By a (discrete) circle we mean a set of
|M| points, one in each leaf of 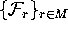 .
The algorithm stops
when the prescribed number N of circles
has been added.
The mesh is stored in
the array
.
The algorithm stops
when the prescribed number N of circles
has been added.
The mesh is stored in
the array Mesh[i][r] of points in
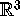 , where
, where i 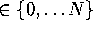 and
and 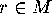 . In other words,
. In other words,
Mesh[i] is a circle of |M| points, and
Mesh[*][r] is a seqence of
N+1 points in the leaf  .
The initial circle
.
The initial circle Mesh[0] is
simply M, and the next circle Mesh[1]
consists of
the points that
are a prescribed initial distance 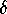 from
M along the linear approximation
from
M along the linear approximation  .
.
During the computation we need
the continuous object
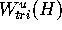 , which is the approximation
of the computed part of
, which is the approximation
of the computed part of  defined as a linear
triangulation of the mesh points.
defined as a linear
triangulation of the mesh points.
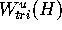 is stored
as the dynamical array of triangles
is stored
as the dynamical array of triangles
Tri. Each
triangle contains three pointers to points
of Mesh and three pointers to
its direct neighbors.
Note that consecutive circles of points in
Mesh define a ring of triangles in Tri of
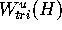 . Consequently,
adding a circle to
. Consequently,
adding a circle to Mesh means adding
a ring to Tri.
Suppose that we want to add a circle to Mesh,
which means that we want to add a new point to
each of the
|M| sequences Mesh[*][r].
Such a point is the next point along the curve
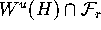 at a prescribed
distance
at a prescribed
distance  from the
last point. The basic idea is to
find a point q in the continuous object
from the
last point. The basic idea is to
find a point q in the continuous object
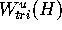 that maps into
that maps into
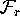 under f
and lies at distance
under f
and lies at distance  from the
last point in
from the
last point in 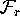 . Since
. Since
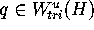 is close to
is close to 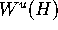 , its image
, its image
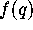 is close to
is close to
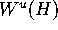 as well. In practical terms, we need
to find the triangle T
in
as well. In practical terms, we need
to find the triangle T
in Tri that contains
q, and then find q by bisection in T.
This works if the distance between
the last circle and its f-image
is at least  ;
see Figure 2 (bottom).
;
see Figure 2 (bottom).
We now give a detailed, more technical description of
the algorithm. It can be found in pseudo-code
in Figure 4
and Figure 5.
Suppose that we have computed
k-1 rings that are stored as a mesh
of k circles in
Mesh[i][r], where i 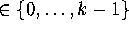 , and
let
, and
let Tri contain all triangles of
the associated triangulation.
The idea is to add a new circle
Mesh[k] of points at a
prescribed distance  from the last circle
from the last circle
Mesh[k-1]. This can be done if the
distance between Mesh[k-1] and its f-image
is at least  ;
compare Figure 2 (bottom).
If this distance is less
than
;
compare Figure 2 (bottom).
If this distance is less
than  we add a new circle at
this smaller distance from
we add a new circle at
this smaller distance from Mesh[k-1].
The latter situation is certain to occur in the
beginning of a computation, when the distance of
Mesh[k-1] to H is still small.
Adding the circle Mesh[k]
to the mesh means that
for all  we need to
find one additional point
we need to
find one additional point
Mesh[k][r] in each sequence
Mesh[*][r].
This new point must lie at distance
 from
from Mesh[k-1][r]
along the unique intersection curve 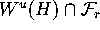 . The idea is to find a point
. The idea is to find a point 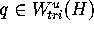 , such that
, such that 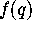 is this new
point in the sequence; see
Figure 6.
Clearly q must
satisfy two conditions: it must
map into
is this new
point in the sequence; see
Figure 6.
Clearly q must
satisfy two conditions: it must
map into 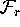 , and it must map
to a point of distance
, and it must map
to a point of distance
 from
from Mesh[k-1][r].
The new point  lies close to
lies close to  ,
because
,
because 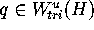 .
.
To find
In most cases, the
intersection
The algorithm GLOBALIZE is shown in pseudo-code in
Figure 4. The procedure MINDIST
computes the minimal distance between
f(
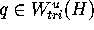 we proceed
as follows. We find a Triangle T, such that
we proceed
as follows. We find a Triangle T, such that
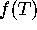 has an intersection with
has an intersection with  ,
and such that there is a point of distance
,
and such that there is a point of distance
 from
from Mesh[k-1][r] in
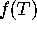 . For reasons of efficiency, one should
start the search for T in
. For reasons of efficiency, one should
start the search for T in Tri at a
guess for T, and then search in the vicinity
of this guess. As a guess we use the
triangle that was found in the previous step
when Mesh[k-1][r] was determined.
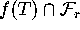 is a single connected curve,
so that T contains
the point q we are looking for.
This situation is sketched in
Figure 7 (top).
By (two-dimensional)
bisection on T the point
is a single connected curve,
so that T contains
the point q we are looking for.
This situation is sketched in
Figure 7 (top).
By (two-dimensional)
bisection on T the point 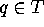 can be found on the curve
can be found on the curve
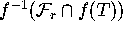 .
The bisection is exact up
to the prescribed bisection tolerance
.
The bisection is exact up
to the prescribed bisection tolerance 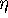 .
We then set
.
We then set
Mesh[k][r] = 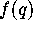 .
It may happen that
.
It may happen that 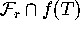 consists
of two separate curves,
so that
consists
of two separate curves,
so that
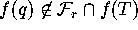 and
and 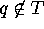 .
Then typically
.
Then typically
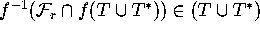 .
Here
.
Here
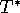 is the (uniquely defined) triangle,
which has the edge with T in common that is not
entered first or exited last
by
is the (uniquely defined) triangle,
which has the edge with T in common that is not
entered first or exited last
by  ; see
Figure 7 (bottom).
In this case, q can be found by
bisection on
; see
Figure 7 (bottom).
In this case, q can be found by
bisection on 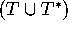 . In our implementation, we
found it sucessful to
always perfom bisection on
. In our implementation, we
found it sucessful to
always perfom bisection on  fo find q.
In case a point q with the mentioned properties
cannot be found, the algorithm stops.
This may be caused by the fact that also
fo find q.
In case a point q with the mentioned properties
cannot be found, the algorithm stops.
This may be caused by the fact that also  consists of disconnected pieces.
If this is indeed the case it is
possible to continue the computation further
by restarting with smaller
consists of disconnected pieces.
If this is indeed the case it is
possible to continue the computation further
by restarting with smaller  .
.
Mesh[k-1]) and Mesh[k-1].
This is done by first
computing the intersections of  with the
f-image of the continuous polygon with vertices
with the
f-image of the continuous polygon with vertices
Mesh[k-1], and then
taking the minimum of the respective distances
in the leaves.
The heart of the algorithm is the procedure
ADDCIRCLE, which returns the new circle
Mesh[k]. Then Tri is updated
by UPDATE, which means that a new ring of
triangles is added to Tri.
ADDCIRCLE is shown in pseudo-code
in Figure 5. The procedure
FINDTRIANGLE returns the triangle T as
specified above, and the procedure
BISECTION returns 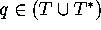 .
This completes the description of the algorithm.
.
This completes the description of the algorithm.
Up: 3. The algorithm
Next: 3.3
The case of a hyperbolic fixed point
Previous: 3.1
Iterating a fundamental domain
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Wed Jul 2 10:51:06 1997