Abstract and Contents

Since the fundamental domain cannot be iterated as a continuous object, one needs to discretize it. As was pointed out earlier, merely iterating the points of the discretiation will lead to a possible accumulation of points on a one-dimensional submanifold of 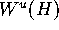; see also Figure 2. In our situation, we can avoid this accumulation by keeping track of where the iterates of the circle intersect 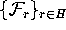. However, there is a second problem. Away from H, the iterates of the initial circle on the linear approximation of 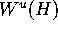may not look like circles at all. In practice, already after a few iterations, the successive images of the fundamental domain may have a very `unpractical' shape. For example in the 3D-fattened Arnold family in Section 5.1, the invariant circle contains two fixed points. Close to the one-dimensional stable manifold of the fixed point that is repelling on H, the f-image of an annulus grows a `nose' that stretches and winds around the circle several times, but at least once. This is unpractical, because it is unclear how one can obtain a nice mesh on the unstable manifold in this situation. It may look like the unstable manifold has holes.

In order to avoid such problems we drop the idea of iterating a fundamental domain. Instead we let the manifold grow at the same speed in each direction, which means that we add rings of fixed width . How this can be done is explained in the following section.

Abstract and Contents

Written by: Bernd Krauskopf & Hinke Osinga
Created: May 27 1997 --- Last modified: Fri May 30 19:49:51 1997