Abstract and Contents

3. The algorithm

We explain the algorithm for computing a two-dimensional unstable manifold of a normally hyperbolic invariant circle of saddle-type. How this algorithm can be used for the case of a hyperbolic fixed point is shown in Section 3.3. We begin by introducing some notation.

Let 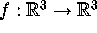be a diffeomorphism with a normally hyperbolic invariant circle H of saddle-type, and let 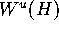be the unstable manifold of H. We assume that f can be transformed to a function defined on 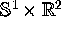, where 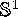is identified with 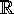, such that H is parametrized over . Then there exist a global linear foliation 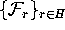that foliates .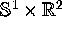

The invariant circle H can be computed by the method in [Osinga 1996, Broer et al. 1996, Broer et al. 1997]. It is represented by a finite mesh M of points on H. The number of points in M can be prescribed. Suppose that the linear foliation satisfies the Foliation Condition. (This is always true in a neighborhood of H; see also Section 6.) Recall that this means that 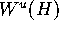intersects each leaf 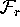in a unique curve. Our goal is to compute an approximation of the unique intersection curve 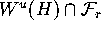for the finitely many leaves of .

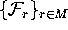To start the algortihm we need to know the first order approximation of 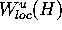in each leaf of 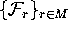. It is defined by unit vectors 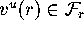that are tangent to 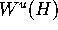. The vectors 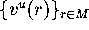can be obtained by interpolation from the embedded unstable normal bundle 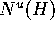that can be obtained from the Df-invariant splitting that is used in the method of [Osinga 1996, Broer et al. 1996, Broer et al. 1997]; see Figure 3. From now on we assume that the starting data for the algorithm, namely M, and 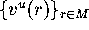, are known.

3.1 Iterating a fundamental domain
3.2 Globalization by adding discrete circles
3.3 The case of a hyperbolic fixed point
3.4 Mesh adaptation

Abstract and Contents

Written by: Bernd Krauskopf & Hinke Osinga
Created: May 27 1997 --- Last modified: Fri May 30 19:49:09 1997