Cross-sections of Beams
The cross section of a beam has a significant effect on how easily the
beam will deform. For example, everyday experience tells us that a
flat metal ruler will flex much more easily than a piece of metal tubing
with walls of the same thickness.
Because it is difficult to use the "shape" of a cross-section directly as a
variable in an equation modeling beam behavior, we instead compute
two quantities that describe properties of the cross
section. These quantities are the centroid and the moment
of inertia , and we will incorporate these
two quantities into our model.
Centroids
If you think of a cross section as a two-dimensional figure cut out of
stiff cardboard, the centroid is the point at which is will balance on
the point of a pin. In many physical settings where the most
important properties are mass and position , the
actual cardboard cross-section will have the same effects as a point
mass located at the centroid. For example, if you are constructing a
mobile, it will balance just as well if you attach a cutout of the
Botticelli's Birth of Venus to one of the arms at her centroid, or
clamp a fishing sinker of equivalent weight there.
Equations modeling physical phenomenon can often be greatly simplified
in situations where a cross-section can be treated as a point mass.
Moment of Inertia
In physical systems where objects are moving and
accelerating, both the mass of the objects and how the mass
is distributed is important. The moment of inertia measures how hard
it is to rotate an object around an axis. Again drawing on every day
experience, it is much easier to twirl an umbrella around when it is
folded than when it is open. The further a mass is from an axis of
rotation, the more it will resist rotating.
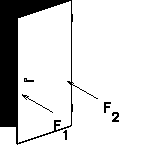
Similarly, a force applied far from the axis of rotation is much more
effective in causing rotation than a force applied close to the axis.
Again drawing on common experience, imagine trying to open a heavy
door. If you push on the door close
to the hinge, then the door will barely budge. It is much easier to
move the door if you push far away from the hinge. That is why door
knobs are placed far away from the door hinges.
To see how the centroid and moment of inertia of a cross section might
effect the way a beam bends, imagine the beam built up out of many
thin cross-sectional slices. Bending the beam amounts to slightly
tilting and sliding the slices. Part of how resistant a beam is to
bending comes from how much each slice resists tilting.
These concepts will be explored in more detail in the sections on Centers of Mass and Centroids and Moments of Inertia.
Return to: Main Ideas.
Last modified: Fri Apr 12 15:45:59 1996