Next: 10 Space Symmetries or Isometries
Up: 9 Coordinate Systems in Space
Previous: 9.4 Relations between Cartesian, Cylindrical, and
Spherical Coordinates
A quadruple of real numbers (x:y:z:t), with t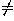 0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t, z/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:z:t) and (x':y':z':t') represent the
same point if and only if there is some real number
0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t, z/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:z:t) and (x':y':z':t') represent the
same point if and only if there is some real number  such that
x'=
such that
x'= x, y'=
x, y'= y, z'=
y, z'= z, t'=
z, t'= t. If P
has cartesian coordinates (x
t. If P
has cartesian coordinates (x ,y
,y ,z
,z ), one set of homogeneous
coordinates for P is (x
), one set of homogeneous
coordinates for P is (x ,y
,y ,z
,z ,1).
,1).
See Section 1.4 for more information on the
relationship between cartesian and homogeneous coordinates. See
Section 10.2 for formulas of space transformations in
homogeneous coordinates.
Next: 10 Space Symmetries or Isometries
Up: 9 Coordinate Systems in Space
Previous: 9.4 Relations between Cartesian, Cylindrical, and
Spherical Coordinates
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
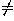 0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t, z/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:z:t) and (x':y':z':t') represent the
same point if and only if there is some real number
0, is a set of
homogeneous coordinates for the point P with cartesian
coordinates (x/t, y/t, z/t). Thus the same point has many sets of
homogeneous coordinates: (x:y:z:t) and (x':y':z':t') represent the
same point if and only if there is some real number  such that
x'=
such that
x'= x, y'=
x, y'= y, z'=
y, z'= z, t'=
z, t'= t. If P
has cartesian coordinates (x
t. If P
has cartesian coordinates (x ,y
,y ,z
,z ), one set of homogeneous
coordinates for P is (x
), one set of homogeneous
coordinates for P is (x ,y
,y ,z
,z ,1).
,1).
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page